ИССЛЕДОВАНИЕ СХОДИМОСТИ АЛГОРИТМА КРИСТОФИДЕСА В ЗАВИСИМОСТИ ОТ ШАГА ШТРАФОВАНИЯ
Секция: 3. Информационные технологии

XII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ИССЛЕДОВАНИЕ СХОДИМОСТИ АЛГОРИТМА КРИСТОФИДЕСА В ЗАВИСИМОСТИ ОТ ШАГА ШТРАФОВАНИЯ
Введение.
Задача коммивояжёра (англ. Travelling salesman problem, сокращённо TSP) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и тому подобное) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов [1].
Совершенно очевидно, что задача может быть решена перебором всех вариантов объезда и выбором оптимального. Но общая постановка задачи, впрочем, как и большинство её частных случаев, относится к классу NP-полных задач. Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе вершин (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет [1].
Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение [1].
Алгоритм Кристофидеса же не является эвристическим. И результатом решения всегда будет оптимальный путь. Данный метод позволяет абстрагироваться от перебора возможных вариантов решения и решить задачу иного рода, что позволяет довольно быстро и максимально точно получить решение задачи коммивояжера. Однако минус данного алгоритма заключается в том, что его сходимость не доказана. Возникают ситуации, когда решение зацикливается и не удается получить ответ. Но изменение стратегии штрафования позволяет выйти из цикла и продолжить решение.
К сожалению, недостаток исследований алгоритма Кристофидеса не позволяет выбрать правильную стратегию штрафования. Данное исследование позволит выбрать изначальный шаг штрафования для последующих исследований, что выделяет его сегодняшнюю актуальность.
Суть алгоритма в том, что преобразование матрицы реберных весов ![]() , при котором различные категории деревьев штрафуются по-разному, но в то же время относительные веса всех деревьев в пределах одной категории не изменяются. Цель при этом состоит в том, чтобы разделить различные категории и сделать категорию гамильтоновых цепей более привлекательной (менее штрафуемой) [2].
, при котором различные категории деревьев штрафуются по-разному, но в то же время относительные веса всех деревьев в пределах одной категории не изменяются. Цель при этом состоит в том, чтобы разделить различные категории и сделать категорию гамильтоновых цепей более привлекательной (менее штрафуемой) [2].
Пусть на входе мы имеем m x n матрицу расстояний dij для графа G. Тогда алгоритм будет состоять из следующих шагов:
· Найти минимальное остовное дерево T с матрицей весов dij;
· Выделить множество N(T) всех вершин нечетной степени в T и найти кратчайшее совершенное паросочетание M в полном графе G с множеством вершин N(T);
· Построить эйлеров граф ![]() с множеством вершин {
с множеством вершин {![]() , … ,
, … ,![]() } и множеством ребер TUM;
} и множеством ребер TUM;
· Найти эйлеров обход ![]() в
в ![]() ;
;
· Построить гамильтонов цикл (соответствующий вложенный тур) ![]() из
из ![]() , последовательным вычеркиванием посещенных вершин [1].
, последовательным вычеркиванием посещенных вершин [1].
Объект и методы исследования.
Объектом исследования было выбрано влияние размера шага штрафования на количество итераций метода которое требуется для получения решения.
Цель исследования — определение оптимального начального шага штрафования для последующих исследований.
За единицу размерности шага штрафования был выбран процент от средней длины ребра.
В работах Николаса Кристофидеса неоднократно упоминается что лучше использовать комбинированный метод штрафования, т. к. он дает лучшие результаты чем положительный и отрицательный методы по-отдельности. Поэтому в нашем исследовании мы использовали комбинированный метод.
Графы были случайно сгенерированы со следующими параметрами:
· Кол-во вершин: 10—50;
· Минимальная степень вершин: 2;
· Максимальная степень вершин: 6—8.
Для исследования алгоритма была реализована программа на языке C#, для рендеринга использовалась система WPF.
Исследование проходило в следующем порядке:
1. Генерация графа по параметрам.
2. Поиск решения для 1 %; Если решение найдено, то ищем решения переходим к шагу 3, иначе к шагу 1.
3. Поиск решения для 2 %; Если решение найдено, то продолжаем поиск с шагом 1 % пока не достигнем верхнюю границу, иначе поиск решения в окрестностях 1 % с шагом 0,5 %.
Результаты исследования.
Таблица 1.
Таблица сходимости метода
Кол-во вершин |
10 |
10 |
20 |
24 |
25 |
26 |
30 |
30 |
30 |
40 |
40 |
50 |
Размер шага, % |
||||||||||||
0,5 |
|
|
|
|
|
|
|
|
|
839 |
|
2297 |
1 |
90 |
59 |
270 |
165 |
116 |
164 |
178 |
69 |
164 |
448 |
330 |
1203 |
1,5 |
|
|
|
|
|
n/f |
|
|
|
n/f |
|
n/f |
2 |
48 |
32 |
146 |
88 |
70 |
n/f |
98 |
41 |
126 |
n/f |
190 |
n/f |
3 |
35 |
n/f |
105 |
63 |
49 |
n/f |
82 |
32 |
141 |
n/f |
144 |
n/f |
4 |
30 |
n/f |
85 |
55 |
n/f |
n/f |
n/f |
28 |
n/f |
n/f |
266 |
n/f |
5 |
22 |
n/f |
66 |
42 |
n/f |
n/f |
n/f |
21 |
n/f |
n/f |
n/f |
n/f |
6 |
17 |
n/f |
63 |
30 |
n/f |
n/f |
n/f |
27 |
n/f |
n/f |
n/f |
n/f |
7 |
18 |
n/f |
54 |
n/f |
n/f |
n/f |
n/f |
23 |
n/f |
n/f |
n/f |
n/f |
8 |
16 |
n/f |
89 |
n/f |
n/f |
n/f |
n/f |
27 |
n/f |
n/f |
n/f |
n/f |
9 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
18 |
n/f |
n/f |
n/f |
n/f |
10 |
13 |
n/f |
49 |
n/f |
n/f |
n/f |
n/f |
14 |
n/f |
n/f |
n/f |
n/f |
11 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
25 |
n/f |
n/f |
n/f |
n/f |
12 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
23 |
n/f |
n/f |
n/f |
n/f |
13 |
90 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
16 |
n/f |
n/f |
n/f |
n/f |
14 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
26 |
n/f |
n/f |
n/f |
n/f |
15 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
25 |
n/f |
n/f |
n/f |
n/f |
16 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
18 |
n/f |
n/f |
n/f |
n/f |
17 |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
n/f |
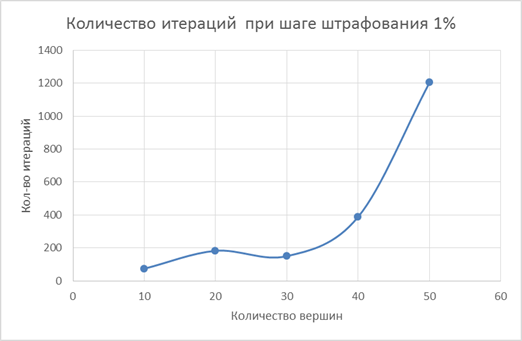
Рисунок 1. График зависимости количества итераций от количества вершин при шаге штрафования 1 %
Данные проведенного исследования показывают, что метод с большей вероятностью сходится при шаге штрафования 1 %. Стоит заметить, что все графы решение которых было невозможно найти с шагом штрафования 1 %, так же не решались с более меньшими шагами штрафования (0,1 %; 0,01 %; 0,001 %).
Заключение.
Результаты проведенного исследования показывают, что для первоначального шага штрафования лучше использовать 1 % от средней длины ребра. Однако не для всех графов находится решение с таким размером и требуется уменьшение шага штрафования.
Также в ходе исследования был построен график зависимости количества итераций от размерности графа. На приведенном графике прослеживается экспоненциальная зависимость. Но несмотря на это, метод все равно показывает колоссальную разницу по времени решения относительно прямого перебора и дает сходное по точности решение.
Список литературы:
1. Википедиия — свободная энциклопедия — [Электронный ресурс] — Режим доступа. — URL: https://ru.wikipedia.org/wiki/Задача _коммивояжёра (дата обращения 11.05.2014).
2. Кристофидес Н. Теория графов: алгоритмический подход / М.: «Мир», 1978.





