АЛГОРИТМЫ АКТИВНОГО ОБУЧЕНИЯ С ЧАСТИЧНЫМ ПРИВЛЕЧЕНИЕМ УЧИТЕЛЯ ДЛЯ РАСПОЗНАВАНИЯ РУКОПИСНЫХ СИМВОЛОВ
Секция: 3. Информационные технологии

II Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
АЛГОРИТМЫ АКТИВНОГО ОБУЧЕНИЯ С ЧАСТИЧНЫМ ПРИВЛЕЧЕНИЕМ УЧИТЕЛЯ ДЛЯ РАСПОЗНАВАНИЯ РУКОПИСНЫХ СИМВОЛОВ
1. Введение
На данный момент существует целый ряд методов машинного обучения на заранее размеченных данных, используемых специалистами в различных областях. Их применяют везде, где возможно применение логики. Они требуют достаточно большого количества таких данных для получения высоких результатов. При этом, на практике, объем неразмеченных данных значительно превышает объем размеченных данных. Например, объемы изображений рукописного текста значительно превышают объемы размеченных изображений символов. В представленной работе показан ряд новых методов с частичным привлечением учителя, для распознавания таких символов. Рассмотрено использование ограниченной машины Больцмана и сверточных нейронных сетей, которые эффективно работают для распознавания рукописных символов. Представленные алгоритмы превосходят классический алгоритм предобучения два хорошо известных алгоритма обучения с учителем.
Существует множество методов обучения для распознавания символов и рукописного текста [1]. Такие алгоритмы, как сверточные сети и нейронные сети, обученные на Ограниченной Машине Больцмана (RBM) достигают наиболее высокой эффективности. Они построены на использовании метода сопряженных градиентов [2]. Оба эти подхода достигают точности близкой к 99 % на MNIST (базы данных рукописных цифр). Однако, как методы обучения с учителем, они также требуют огромного количества размеченных данных для достижения высокой производительности в связи с их сложностью. Размеченные данные, хотя и чрезвычайно полезны, но не всегда могут быть легко получены. Метки как правило, должны быть назначены вручную, а это дорогостоящий и трудоемкий процесс. К сожалению, для рукописного распознавания текста помеченные данные трудно найти, но к счастью, существует большой резерв неразмеченных данных. Эта нехватка размеченных данных в сочетании с обилием неразмеченных приводит к поиску методов, которые используют оба вида этих данных.
Для этого необходимо пересмотреть вышеупомянутые методы обучения с учителем на предмет возможности их модификации для частичного привлечения учителя. Несмотря на то, что существует множество возможных методов с частичным привлечением учителя, они обычно используют априорно размеченные данные.
Было бы намного полезнее, если бы мы могли получить метки этих данных, которые при помощи алгоритма сами добивались высокой эффективности. При такой реализации возможно дообучать алгоритм в режиме реального времени по распознаваемым данным. Такой подход называется активным обучением [3].
2. Методы с учителем
2.1 Сверточные сети
Сверточные сети используют две основные техники, для создания классификаторов инвариантных к искажению. Они используют детекторы особенностей, для того, чтобы преобразовать сырые данные. Эти детекторы состоят из группы весов, которые применяются к группе входных данных в небольшой окрестности. Применяя разные наборы детекторов особенностей, выделяются разные поля восприятия данных. Другая техника, которая используется в сверточных сетях — децимация. Так как точное положение особенностей не всегда важно, сверточные сети используют децимацию, которая состоит из усреднения и прореживания. Это приводит к уменьшению размерности карты особенностей, а так же к меньшей чувствительности к сдвигам и искажениям.
Обычно сверточные сети имеют несколько слоев, состоящих из определения особенностей и децимаций, изменяющихся между слоями.
2.2 Предобучение нейронной сети с использованием RBM
Джофри Хинтон с соавторами показал [3], что эффективность нейронной сети может быть существенно улучшена, если начальные веса инициализируются с использованием RBM, и после этого уточняются с помощью метода обратного распространения ошибки. С помощью предобучения нейронная сеть (с множеством скрытых слоев) может обойти проблему начальной инициализации весов. Сети такого класса будут требовать начальных весов, близких к приемлемому решению.
Каждая пара соседних слоев в сети обучается с помощью RBM. Доступные данные поступают на вход RBM, которая изменяет веса, чтобы уменьшить энергию сети для представленных данных. Этот метод повторяется для весов всех слоев сети.
3. Методы с частичным привлечением учителя
3.1 Упрощенный общий алгоритм
Это довольно простой алгоритм с частичным привлечением учителя, который будет использовать активное обучение опираясь на алгоритм кластеризации K-средних и классификатор K-ближайших соседей. Исходные данные, которые не размечены, используются для того, чтобы определить K-кластеров. В качестве функции расстояния обычно используются Евклидово расстояние. Зная разбиение на кластеры, из всех данных отбираются те, которые находятся ближе к центрам своих кластеров. Такие более точные кластеризованные данные передаются экспертам, для дальнейшей корректировки. Когда эксперты размечают эти данные, то оставшиеся данные размечаются автоматически с помощью классификации по ближайшему соседу. Несмотря на кажущуюся простоту алгоритма, он значительно превосходит более сложные методы обучения с учителем, благодаря использованию больших наборов данных. Кроме того, этот простой алгоритм может быть улучшен помощью техник описанных далее, одной из которых является использование активного обучения.
3.2 Использование автоэнкодера с частичным привлечением учителя
Метод, представленный в предыдущем пункте, может быть улучшен с использованием автоэнкодера. Кроме того, автоэнкодеры могут быть использованы совместно с RBM. Автоэнкодеры позволяют создать сеть с небольшим числом нейронов в центральном слое. Это позволяет сделать нейронную сеть менее чувствительной к искажениям данных, а так же достигнуть снижения их размерности. Автоэнкодер представляет собой симметричную нейронную сеть, обучаемую таким образом, чтобы входные и выходные данные совпадали. Средний уровень содержит столько нейронов, как и внутренняя размерность представления данных, которых мы хотим достичь.
Чтобы скомбинировать автоэнкодер, обучение с частичным привлечением учителя, и активное обучение, сначала обучается авоэнкодер на исходных неразмеченных данных. После того, как он обучен, для кластеризации можно использовать значение нейронов среднего слоя тем же способом, который был описан выше.
3.3 Аналогии для сверточных сетей
В предыдущих пунктах было показано, как с помощью относительно простого способа можно получить алгоритм обучения с частичным привлечением учителя на основе нейронных сетей предобученных на RBM. Для сверточных сетей не существует такого простого обобщения, на случай с частичным привлечением учителя. Для того, чтобы обойти эту проблему необходимо переопределить две базовых техники: определение особенностей и децимацию, так, чтобы они могли быть использованы для работы с неразмеченными данными.
В статьях различных авторов существует несколько решений данной проблемы. В данной статье мы рассмотрим сложный, но, тем не менее, весьма логичный выход из описанной выше проблемы. Для того, чтобы адаптировать сверточную нейронную сеть к неразмеченным данным, можно воспользоваться автоэнкодером.
3.4 Сверточные автоэнкодеры
Мы можем попытаться решить проблему обучения сверточных сетей на неразмеченных данных с использованием автоэнкодеров. Так как сверточные сети, по сути, представляют собой обычную многослойную нейронную сеть с определенными ограничениями, то эти сети подразумевают построение симметричных уровней. Каждая пара слоев нейронов, симметричных относительно среднего уровня будет обладать одинаковыми связями, при этом их матрицы весов будут связаны через операцию транспонирования. Применение такого типа нейронной сети, позволяет обучать сверточную нейронную сеть также, как если бы это был простой автоэнкодер. Кроме того, возможно использовать RBM между каждой парой соседних слоев для предобучения.
Основным минусом такой системы является необходимость использования большого объема исходных неразмеченных данных. Основное достоинство такой системы заключается в том, что она способна обработать и обучиться на очень большом объеме неразмеченных данных и показать наилучший результат среди всех вышеописанных техник. Описание алгоритма изображено на рис. 1, где: ![]() — матрица весов нейронов,
— матрица весов нейронов, ![]() — транспонированная матрица.
— транспонированная матрица.
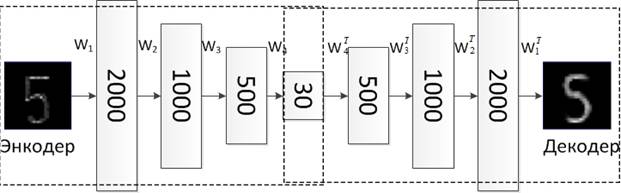
Рисунок 1. Принцип работы автоэнкодера
Результаты
Тестирование алгоритмов распознавание символов рукописного текста проводилось на базе символов MNIST. Кроме того что база является размеченной, для обучения методов с частичным привлечением учителя использовались большие (>50000 символов) наборы неразмеченных данных.
Таблица 1
Сравнение ошибок при тестировании на различных алгоритмах
Название алгоритма |
Ошибка при тестировании (%) |
Сверточные автоэнкодеры |
0,39 % |
Ограниченная Машина Больцмана |
1,25 % |
Нейронная сеть 1000 нейронов |
~1,6 % |
Нейронная сеть 500 -->300 нейронов |
~1,6 % |
K-Ближайших Соседей |
~ 3,3 % |
Машина Опорных Векторов |
1,4 % |
Наилучший результат показывает алгоритм обучения сверточной нейронной сети с частичным привлечением учителя на базе автоэнкодера.
На втором месте находится Ограниченная Машина Больцмана, требующая большой базы размеченных данных. Это внушает уверенность, что дальнейшие успехи в этой области будут достигнуты объединением этих двух техник.
Выводы
В статье рассмотрены современные методы обучения нейронной сети на размеченных данных и неразмеченных данных с частичным привлечением учителя. Наилучшим алгоритмом распознавания по результатам тестирования можно назвать многослойную сверточную нейронную сеть. В дальнейшем планируются исследования в рамках практического применения рассмотренных алгоритмов для распознавания в условиях реальных шумов и искажений, внесенных алгоритмами сжатия данных.
Список литературы:
1. A. Vinciarelli. Of_ine cursive handwriting: From word to text recognition. Technical Report IDIAP-RR03-24, Dalle Molle Institute for Perceptual Arti_cial Intelligence, 2003.
2. G.E. Hinton and R.R. Salakhutdinov. Reducing the dimensionality of data with neural networks. Science, 313 (5786):504.507, 2006.
3. D.A. Cohn. Neural network exploration using optimal experiment design. In J. Cowan, G. Tesauro, and J. Alspector, editors, Advances in Neural Information Processing Systems 6, pages 679.686. San Mateo, CA: Morgan Kaufmann, 1994.





