ЗАДАЧА УПАКОВКИ ДВУХ ШАРОВ В ЕДИНИЧНЫЙ КУБ
Секция: Физико-математические науки

LXI Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
ЗАДАЧА УПАКОВКИ ДВУХ ШАРОВ В ЕДИНИЧНЫЙ КУБ
THE PROBLEM OF PACKING TWO BALLS INTO A UNIT CUBE
Dina Gergenova
Student of 10 M (physics and mathematics) class MBOU lyceum No. 3, Russia, Irkutsk
Mikhail Perfiliev
Scientific adviser, Doctor of the International Academy of Natural Sciences, Russia, Irkutsk
Аннотация. Данная работа посвящена задаче о максимально плотной упаковке двух шаров в единичный куб. Двумя различными способами найдены радиусы двух шаров. При этих значениях радиусов суммарный объем шаров принимает наибольшее значение. В качестве инструментов решения задачи использованы элементы логики, аналитической геометрии, а также программное решение этой проблемы на классическом компьютере.
Abstract. This work is devoted to the most dense packing of two balls into a unit cube. The radii of two balls are found in two different ways. With these values of radii, the total volume of these balls is the largest. Some elements of logic, analytical geometry, as well as a software solution with a classical computer are used as tools for solving the problem.
Ключевые слова: задачи упаковки, единичный куб, шар, сфера, язык программирования С++
Keywords: packing problems, unit cube, ball, sphere, programming language C++
Введение
Задачи упаковки являются задачами оптимизации в геометрии, суть которых состоит в упаковке объектов в контейнеры [1]. Поставим следующую задачу. В куб со ребром единичной длины поместили два шара. При каких значениях радиусов шаров суммарный объем, занимаемый ими, будет наибольшим? Логично предположить, что наибольший суммарный объем шаров получим при максимальном их удалении друг от друга. Значит центры этих шаров должны лежать на объемной диагонали куба. Также логично предположить, что радиус одного из этих шаров должен быть наибольшим, то есть равным 0,5, и шары должны касаться друг друга (Рис.1.) . Уравнение большей сферы запишется как
![]() , (1)
, (1)
где ![]() - ее центр, R – ее радиус. Тогда объем шара, ограниченного этой сферой, равен
- ее центр, R – ее радиус. Тогда объем шара, ограниченного этой сферой, равен
![]() . (2)
. (2)
Уравнение меньшей сферы запишется в форме
![]() , (3)
, (3)
где ![]() - ее центр, r – ее радиус. Объем шара, ограниченного этой сферой, равен
- ее центр, r – ее радиус. Объем шара, ограниченного этой сферой, равен
![]() . (4)
. (4)
[2]
Так как центры шаров лежат на объемной диагонали куба, то их координаты будут соответственно равны
![]() ;
; ![]() , (5)
, (5)
если начало декартовой системы координат разместить в вершине куба, ближней к малому шару.
Шары касаются друг к друга, поэтому расстояние между их центрами должно быть равно сумме из радиусов. Пользуясь формулой расстояния между двумя точками [3], составим уравнение:
![]() (6)
(6)
откуда находим значение r:
![]() ;
;
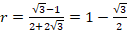 ;
; ![]() . (7)
. (7)
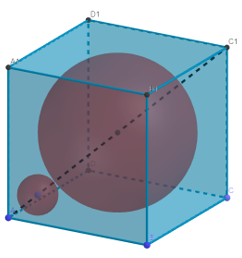
Рисунок 1. Максимально плотная упаковка двух шаров в куб.
Формальное решение задачи упаковки двух шаров в куб
Подтвердим логику рассуждений при помощи компьютерной программы, составленной на языке программирования C++ [4],[5] :
#include <iostream>
//подключаем библиотеку, реализующую основы ввода и вывода информации
#include <cmath>
//подключаем библиотеку с математическими функциями
using namespace std;
//директива позволяет использовать ввод данных cin>> и вывод данных на экран //cout<<
int main()
//точка входа в программу
{
int x,y,z,a,b,c,r,rr,R,RR,V;
//координаты центра первого шара (x;y;z), координаты
// центра второго шара (a;b;c), варьируемые радиусы шаров R и r, искомые //радиусы RR и rr, суммарный объем шаров V имеют целочисленный тип
V=0;
//начальный суммарный объем задаём нулевым
for (x=0;x<=10;x++)
{for (y=0;y<=10;y++)
{for (z=0;z<=10;z++)
{for (a=0;a<=10;a++)
{for (b=0; b<=10;b++)
{for (c=0; c<=10;c++)
{for (R =0;R<=5;R++)
{for (r=0; r<=5;r++)
//координаты центров шаров варьируются от 0 до 10 с шагом 1, радиусы шаров // варьируются от 0 до 5 с шагом 1
{if (x-r>=0 && x+r<=10 && y-r>=0 && y+r<=10
&& z-r>=0 && z+r<=10 && a-R>=0 && a+R<=10
&& b-R>=0 &&b+R<=10 && c-R>=0 && c+R<=10
&& pow(a-x,2)+pow(b-y,2)+pow(c-z,2)>=pow(R+r,2)
&& pow(R,3)+pow(r,3)>V)
//требуем, чтобы шары не выходили за границы куба и не пересекались, то есть // не были частично или полностью погружены друг в друга
{V=pow(R,3)+pow(r,3);
RR=R;
rr=r;}
//максимизирует объем и фиксируем соответствующие ему искомые радиусы //большого и маленького шаров
}
}
}
}
}
}
}
}
cout<<"Больший радиус"<<RR<<endl<<"меньший радиус"<<rr;
//выводим больший и меньший радиусы на экран, причем в разных строках
return 0;
//возращение нуля в систему как критерий правильности работы программы
}
Для простоты расчетов ребро куба увеличили в 10 раз. При максимизации суммарного объема в программе не учитывали множитель ![]() , так как достаточно потребовать максимизации суммы кубов радиусов.
, так как достаточно потребовать максимизации суммы кубов радиусов.
Программа выдает значение большего радиуса 5 (что соответсвует значению R=0,5 для единичного куба) и значение малого радиуса 1 (для единичного куба 0,1, так как в программе мы задали целочисленный тип для r. Истинное значение r равно ![]() ).
).
Заключение
Таким образом, в данной работе дано логически-алгебраическое и формальное решение задачи о наиболее плотной упаковке двух шаров в куб с единичным ребром. Найдены радиусы шаров, при которых доля занимаемого ими пространства будет максимальной. Для формального решения задачи составлена программа на одном из самых мощных и популярных языков программирования в мире — С++.





