Высокоскоростные генераторы псевдослучайных двоичных последовательностей на основе клеточных автоматов

Псевдослучайные числовые последовательности имеют широкое применение во многих областях: численный анализ, моделирование, проектирование игр, программирование, криптография. Особую роль в криптографии играют двоичные последовательности, на которых будет сделан акцент в данной работе. Каждый из алгоритмов генерации псевдослучайных последовательностей имеет те или иные недостатки, поэтому разработка и реализация новых генераторов псевдослучайных последовательностей (ГПСП) с хорошими статистическими показателями и высоким быстродействием является актуальной теоретической и прикладной научной задачей.

Идея клеточных автоматов была предложена в конце 40-х годов XX века и нашла свое применение во многих областях науки, в том числе и в криптографии. Клеточный автомат — дискретная модель, состоящая из регулярной решётки ячеек любой размерности, каждая из которых может находиться в одном из конечного множества состояний, таких как 1 и 0. Для каждой ячейки определено множество ячеек, называемых окрестностью. Для работы клеточного автомата требуется задание начального состояния всех ячеек и правил перехода ячеек из одного состояния в другое. На каждой итерации, используя правила перехода и состояния ячеек окрестности, определяется новое состояние каждой ячейки [3].

Также немалое значение для криптографии имеют булевы функции, обладающие нелинейными свойствами. Чаще всего наибольший интерес представляют те булевы функции, для которых эти свойства экстремальны. Такие булевы функции носят название бент-функций [7]. Начало их активного исследования датируется 60-ми годами XX века.

Целью работы является создание генератора псевдослучайных двоичных последовательностей на основе клеточных автоматов и бент-функций, программная реализация данного автомата и исследование криптографических свойств и быстродействия данного генератора.

За основу был взят генератор из статьи [6], который был дополнен и модифицирован для удобства программной реализации и улучшения быстродействия и стохастических свойств вырабатываемых последовательностей. Под стохастичностью понимается случайность результирующих последовательностей. Четыре инициализационные и Mg-последовательность являются ключом генератора и вырабатываются до начала его работы и подаются ему на вход.  Mg-последовательность обладает свойствами сбалансированности и k-граммного распределения [6]. Под сбалансированностью понимается условие, при котором число символов «0» и символов «1» в последовательности равны или чрезвычайно близки [5]. Свойство k-граммного распределения означает, что каждая серия из k бит встречается на замкнутом цикле точно один раз [5]. Использование Mg-последовательности помогает противостоять таким инициализационным последовательностям, которые могут приводить к плохим стохастическим свойствам генерируемой последовательности или же останавливать эволюцию автомата переходом в стационарные или периодические во времени конфигурации [5].

Алгоритм 1. Вычисление ключа генератора:

Вход: Целое число L – длина вырабатываемых последовательностей.

Выход: 5 двоичных псевдослучайных последовательностей (ПСП) длины L (четыре инициализационные S₀₁, S₀₂, S₀₃, S₀₄ и одна Mg-последовательность).

Шаг 1. С помощью встроенного генератора случайных чисел создается четыре инициализационных двоичных ПСП S₀₁, S₀₂, S₀₃, S₀₄ длины L.

Шаг 2. С помощью встроенного генератора случайных чисел создается ПСП Mg.

Шаг 3. Проверяется свойство сбалансированности для последователь-ности Mg. Добиться равенства количества нулей и единиц в последовательности большой длины (в криптографических приложениях используются последовательности длины порядка 2¹⁰ и больше) довольно проблематично и не является необходимым, поэтому, если в последовательности отношение количества нулей к количеству единиц лежит в промежутке от 0,999 до 1.001, то она принимается как сбалансированная. Если последовательность Mg не проходит проверку на сбалансированность, то возвращаемся в шаг 2.

Шаг 4. Проверяется свойство k-граммного распределения для последо- вательности Mg. Данная проверка сводится к подтверждению того факта, что в последовательности не содержатся блоки из одних нулей или одних единиц длины больше, чем log₂ L [5]. Если последовательность не проходит данную проверку, возвращаемся в шаг 2.

Шаг 5. Записываем в файл ключа последовательности S₀₁, S₀₂, S₀₃, S₀₄ и Mg.

Фактически, на выходе имеем ключ длины 5 * L, так как он состоит из 5 последовательностей длины L. Однако для простоты за длину ключа будем принимать именно число L.

Алгоритм 2. Нахождение хэш-значения для двоичной последовательности:

Вход: Двоичная последовательность S.

Выход: Целое число H – хэш-значение для последовательности S.

Шаг 1. Присваиваем H := 0, L = длина последовательности S.

Шаг 2. Пробегая по всей последовательности S, увеличиваем значение H на 1, если значение рассматриваемой ячейки равно 1.

Шаг 3. Присваиваем L’ := L % 10.

Шаг 4. Пробегаем 10 ячеек S[i * L’] последовательности S, где 1 ≤ i ≤ 10, и прибавляем к значению H число 100, если значение рассматриваемой ячейки S[i * L’] равно 1.

Шаг 5) Присваиваем H := H (mod L) и выводим H в ответ.

Данный метод нахождения хэш-значения не защищен от коллизий, однако для нашей подзадачи, в которой данный метод будет применяться, это не является существенным фактором. 

Алгоритм 3. Генерация двоичных псевдослучайных последовательностей:

Вход: Целое число N – количество ПСП для генерации, ключ (S₀₁, S₀₂, S₀₃, S₀₄, Mg) из 5 последовательностей длины L (4 инициализационные S₀₁, S₀₂, S₀₃, S₀₄ и одна Mg-последовательность).

Выход: N двоичных псевдослучайных последовательностей длины L.

Шаг 1. Создается 4 потока, каждый из которых будет генерировать N % 4 последовательностей.

Шаг 2. На вход каждому из четырех потоков подается соответствующая инициализационная последовательность S_0i и Mg-последовательность.

Шаг 3. Пробегая по каждому биту b_j (0 < j ⩽ L) последовательности S_0i (зацикленной), отбираем три его левых и три правых соседа. Помещаем полученные 6 значений в одну из двух бент-функций от 6 переменных, которая выбирается в соответствии со значением рассматриваемого бита («0» - первая функция, «1» - вторая). Результат бент-функции записываем вместо b_j. В итоге получаем последовательность S_1i.

Шаг 4. Складываем S_1i и Mg побитовым сложением по модулю 2, получаем S_2i.

Шаг 5. С помощью алгоритма 3 находим целочисленное хэш-значение H для последовательности S_2i и производим циклический сдвиг последовательности S_2i на H бит вправо.

Шаг 6. Выводим последовательность S_2i в ответ. Если уже выведено N % 4 последовательностей, то поток завершает свою работу. Иначе подаем S_2i на вход тому же потоку вместо S_0i и проходим еще один цикл генерации.

Каждый поток сгенерирует N % 4 последовательностей и запишет их в выходной файл в соответствии со своим порядком (первые N % 4 последовательностей сгенерированы первым потоком, вторые N % 4 последовательностей – вторым, и т.д.). В итоге, имеем N псевдослучайных двоичных последовательностей длины L.

Период генератора будет определяться его ключом. Имеются 4 последовательности длины L и одна Mg-последовательность. Мощность множества Mg-последовательностей каждый раз будет отличаться в зависимости от L, поэтому данное значение сложно учесть. Ограничимся оценкой снизу. Инициализационные последовательности генерируются с помощью класса Random пространства имен System (в языке C#), который имеет период 2³² [8].  Ключ состоит из 4 таких последовательностей (не учитывая Mg-последовательность), поэтому суммарный период составит (2³²)⁴ = 2¹²⁸. Такой период является приемлемым для использования в криптографических целях.

В ходе работы создана программная реализация описанного ГПСП на языке C# в среде Microsoft Visual Studio 2017 Enterprise Edition.

Тестирование быстродействия генератора осуществляется на вычислительной машине с процессором Intel(R) Core(TM) i5-5257U CPU 2.70 GHz. Для определения быстродействия и производительности генерируются 1000 двоичных ПСП длиной 102400 бит. Создание ключа (генерация четырёх инициализационных и одной Mg-последовательности длиной 1024 бит) заняло 7 миллисекунд, то есть производительность генерации ключа составила 17,9 Мбит/с. После этого на данном ключе была запущена генерация 1000 последовательностей, которая была осуществлена за 8 секунд 75 миллисекунд без учета времени записи результата генерации в файл (чрезвычайно затратная операция записи в файл в криптографических приложениях зачастую не применяется – генерируемые псевдослучайные последовательности сразу каким-либо образом применяются и отбрасываются). Таким образом, производительность данного процесса составила 1,4 МБ/с или 11,88 Мбит/с.

Одними из важных криптографических характеристик клеточного автомата являются характеристики лавинного эффекта. Лавинный эффект представляет собой способность динамической системы существенно изменять выходную последовательность при небольших изменениях входных данных. Это означает, что все выходные биты зависят от каждого входного бита.  Понятие лавинного эффекта было официально введено Х. Фейстелем в 1973 году [1], однако, концептуальное понятие уже до этого было использовано Шенноном. Оценка лавинного эффекта заключается в подаче на вход клеточного автомата двух двоичных последовательностей, одна из которых отличается от второй значением одного единственного бита, и сравнение возникающей разницы на каждом следующем такте работы клеточного автомата. Рассматриваются две характеристики лавинного эффекта – интегральная и пространственная. Интегральной характеристикой  лавинного эффекта называется зависимость доли несовпадающих ячеек у двух конечных автоматов от номера такта t [4]. Пространственной характеристикой μ лавинного эффекта называется зависимость отношения расстояния от вершины с номером 0 до самой дальней вершины, ячейка которой у двух автоматов не совпадает, к эксцентриситету вершины с номером 0 (то есть к расстоянию от вершины с номером 0 до самой дальней вершины) [4]. Для обеспечения хороших статических характеристик выходной последовательности необходимо, чтобы лавинный эффект был близок к оптимальному. Для этого значение интегральной характеристики должно максимально быстро приближаться к значению 0.5, а значение пространственной – к значению 1 [4]. Результаты исследования лавинного эффекта автомата, лежащего в основе описанного генератора, представлены на следующих графиках:

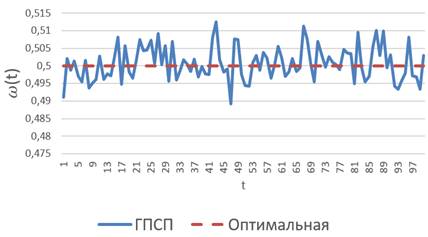
Рисунок 1. Интегральная характеристика лавинного эффекта клеточного автомата

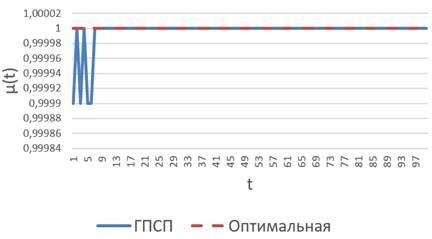
Рисунок 2. Пространственная характеристика лавинного эффекта клеточного автомата

По графикам видно, что автомат, лежащий в основе ГПСП, имеет лавинный эффект, чрезвычайно близкий к оптимальным значениям как по интегральной характеристике ( (t) = 0,5), так и по пространственной (μ(t) = 1).

Финальным шагом оценки разработанного генератора является тестирование стохастических свойств вырабатываемых последовательностей. Для этого используется набор статистических тестов NIST Statistical Testing Suite of Random Number Generators (NIST STS), разработанный Национальным институтом стандартов и технологий США (ITL NIST) [2]. Результатом работы NIST STS является краткий отчет следующего вида:

Рисунок 3. Начальный фрагмент краткого отчета с результатами тестирования

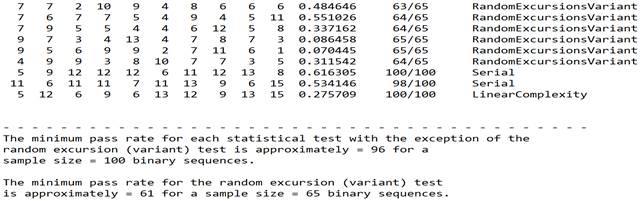
Рисунок 4. Конечный фрагмент краткого отчета с результатами тестирования

В конце данного отчета видны требования для успешности прохождения тестирования – результат должен быть не ниже 96/100 для тестов со 100-бальной системой оценки и 61/65 для тестов с 65-бальной системой оценки. В полученном отчете все тесты удовлетворяют данному требованию, поэтому следует признать качество вырабатываемых последовательностей генератора достаточным для использования в криптографических целях.

Таким образом, итогом данной работы является разработка и программная реализация быстродействующего генератора псевдослучайных двоичных последовательностей на базе клеточного автомата с близким к оптимальному лавинным эффектом, а вырабатываемые данным генератором последовательности отвечают самым высоким требованиям, что позволяет применять генератор в современных криптографических приложениях.