Анализ системы управления приводом электромеханического подъемника
Секция: Технические науки
лауреатов
участников
лауреатов


участников



I Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Анализ системы управления приводом электромеханического подъемника
Электрический двигатель – ядро современных приводов, приводящих в движение разнообразные технологические машины. Современный электропривод представляет собой сочетание электродвигателей, систем передачи и средств управления, обеспечивающих автоматизированную работу производственных машин. Эта работа совершается с требуемой закономерностью при преобразовании электрической энергии в механическую.
Целью данной работы является анализ динамической системы, а именно привода электромеханического подъемника.
Для достижения поставленной цели будут решаться следующие задачи:
1. Исследование математической модели системы;
2. Исследование математической модели системы в пространстве состояний;
3. Исследование системы на управляемость и наблюдаемость;
4. Построение временных характеристики динамической системы;
5. Построение частотных характеристик динамической системы.
Динамической системой принято называть множество элементов, для которого задана функциональная зависимость между временем и положением в пространстве каждого элемента системы. Данная математическая абстракция позволяет изучать и описывать эволюцию систем во времени.
Структурная схема исследуемой системы представлена на рисунке 1.
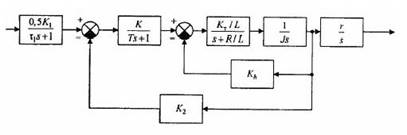
Рисунок 1. Структурная схема исследуемой системы управления
Исследование математической модели
Для проведения анализа исследуемой системы необходимо получить эквивалентную передаточную функцию, составленную путем свертывания имеющихся соединений динамической системы.
Зададим следующие значения коэффициентов передаточных функций (ПФ):
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Подставив их в ПФ и выполнив свертывания соединений, получим эквивалентную ПФ:
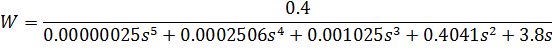
Одними из основных свойств динамических систем при их анализе является их устойчивость - свойство системы возвращаться в исходное состояние равновесия или вынужденного движения после снятия внешнего воздействия на систему.
Характеристиками динамических систем являются ее нули (комплексные числа, являющиеся корнями полинома числителя эквивалентной ПФ) и полюса (комплексные числа корней полинома знаменателя эквивалентной ПФ). В данном случае передаточная функция не содержит нулей, но имеет следующие полюса:

Исходя из полученных результатов, можно сделать вывод о неустойчивости динамической системы, так как полюса ПФ имеют корни с положительной действительной частью. Так как система является не устойчивой, время переходного процесса (характеристика, показывающая динамические свойства системы, время, за которое выходной сигнал системы окажется внутри 5-ти процентного «коридора» от установившегося значения) определить нельзя.
Исследование математической модели в пространстве состояний
Для любой динамической системы можно определить некоторую совокупность переменных ![]() , способная в полной мере характеризовать состояние системы в любой момент времени. Такие переменные получили название переменных состояния динамической системы.
, способная в полной мере характеризовать состояние системы в любой момент времени. Такие переменные получили название переменных состояния динамической системы.
Некоторая область возможных значений переменных состояния называется пространством состояний динамической системы. Количество независимых переменных ![]() , характеризующих состояние системы, определяет размерность пространства состояний [1].
, характеризующих состояние системы, определяет размерность пространства состояний [1].
В общем виде динамическую систему можно описать в пространстве состояний следующим обобщенным уравнениями вида:

Для исследуемой системы матрицы коэффициентов модели в пространстве состояний будут следующими:

Модель в пространстве состояний имеет следующие достоинства:
· Описание объекта является универсальным;
· Переменные состояния могут выбираться произвольным образом;
· Математически методы расчета не изменяются в зависимости от числа переменных, количества входных и выходных сигналов.
Исследование динамической системы на управляемость и наблюдаемость
Управляемостью принято называть возможность изменения состояния системы с помощью некоторых внешних воздействий. Матрица управляемости находится по формуле: ![]() где n – ранг матрицы.
где n – ранг матрицы.
Для того чтобы динамическая система была полностью управляемой, необходимо и достаточно, чтобы матрица управляемости системы
R имела ранг, равный n. В нашем случае ранг матрицы R равен 5. Следовательно, данная динамическая система управляемая.
Наблюдаемость характеризует возможность определения состояния системы по наблюдениям за ее выходными сигналами. Матрица наблюдаемости находится по формуле: ![]() где n – ранг матрицы.
где n – ранг матрицы.
Для того чтобы динамическая система была полностью наблюдаемой, необходимо и достаточно, чтобы матрица наблюдаемости системы Q имела ранг равный n. В нашем случае ранг матрицы Q равен 5. Следовательно, система наблюдаема.
Построение временных характеристик динамической системы
Временные характеристики динамической системы представляют собой зависимость выходного сигнала от времени при подаче на ее вход некоторого типового воздействия
Имея модель динамической системы в пространстве состояний, можно получить соответствующую ей передаточную функцию, используя следующее соотношение:
![]()
ПФ будет иметь вид:

На рисунке 2 представлена переходная характеристика (реакция динамической системы на единично ступенчатую функцию) динамической системы.

Рисунок 2. График переходной характеристики динамической системы
Показатели качества переходного процесса являются перерегулирование и время переходного процесса, которые в данном случае невозможно вычислить:
Частотные характеристики динамической системы
Одними из основных частотных характеристик являются АЧХ, ФЧХ. Данные характеристики можно представить в виде графиков (рисунок 3).
Амплитудная частотная характеристика (АЧХ) – зависимость амплитуды колебания на выходе устройства от частоты входного гармонического сигнала. Измеряется по изменению частоты постоянного по амплитуде входного сигнала:
![]()
Фазо-частотная характеристика (ФЧХ) – зависимость сдвига фаз между вынужденными колебаниями системы и гармоническим возбуждением с постоянной амплитудой от частоты последнего: ![]() .
.
Запас устойчивости по амплитуде и по фазе можно найти по графику, представленному на рисунке 3.

Рисунок 3. Графики АЧХ и ФЧХ (слева) и запаса устойчивости (справа)
Согласно графику, запас устойчивости по фазе Pm = 89.4, а по амплитуде Gm = inf.
Частотные характеристики достаточно часто используются на практике, так как они могут быть получены экспериментальным путем без построения математической модели исследуемой системы.
Список литературы:
1. Методы классической и современной теории автоматического управления: учебник в 5 томах; 2-е изд., перераб. и доп. Т. 1: Математические модели, динамические характеристики и анализ систем управления – Москва: Издательство МГТУ им. Н.Э. Баумана, 2004, - 656 с.

