Составление экономико-математической модели задачи о рационе питания

Диета – это особым образом подобранный рацион по количеству питательных веществ, а также режим питания для достижения определенных целей (снижения веса, набора веса, улучшения состояния здоровья). Главным в составлении диетического питания являются положенные научно обоснованные физиологические нормы питания. В соответствии с ними питание человека должно удовлетворять его физиологические потребности в питательных веществах и энергии. Основные питательные вещества (белки, жиры, углеводы), а также прочие необходимые компоненты (витамины) должны поступать в организм в нужном количестве в соответствии с нуждами определенного человека. Физиологические потребности в количестве и времени приема необходимых питательных веществ зависят от большого количества факторов: пола, возраста, состояния здоровья, веса тела, физической активности и т.д. Все эти факторы необходимо учитывать при создании правильного рациона питания. Разнообразие продуктов питания сильно усложняет процесс создания диеты, делая его практически невозможным без применения математических методов [1].

Также разработка рациона питания необходима при составление кормовой базы в сельском хозяйстве при выращивании скота. При создании рациона кормления домашнего скота необходимо учитывать нормы количества употребляемого корма и количество содержащихся в нем питательных веществ. Кормовую базу необходимо сформировать так, чтобы рацион кормления скота был составлен из нескольких составляющих и включал в себя сбалансированный рацион сочных, грубых и концентрированных кормов, который должен содержать все необходимые питательные вещества для организма. Необходимо сбалансировать протеин, незаменимые аминокислоты, витамины и минеральные вещества. Нехватка микроэлементов и минеральных веществ в рационе (натрий, кальций, фосфор и др.) компенсируется путем применения специальных добавок. При недостатке или избытке хотя бы одного элемента рациона питания ухудшается эффективность использования питательных веществ всего рациона скота.

Для составления рациона питания требуется рассчитать суточную диету, т.е. количество каждого продукта Р_j, чтобы, с одной стороны, обеспечить минимально необходимое количество питательных веществ, а с другой − минимизировать стоимость разработанной диеты.

Для того, чтобы облегчить выполнение вышеперечисленных целей составляется экономико-математическая модель задачи о диете. В общем виде данная модель выглядит следующим образом.

х_j (j = 1, 2,…, n) – количество j-го продукта в дневном рационе. В рационе используется n видов продуктов. Каждый продукт содержит m необходимых питательных веществ в количестве не менее b_i (i = 1,2,…,m) единиц, a_ij – число единиц необходимого питательного вещества B_i в единице продукта j-го вида. Известна стоимость c_j единицы j-го продукта. Необходимо составить рацион нужной питательности при минимальных затратах на него.

Для решения поставленной задачи необходимо сформулировать её математическую модель, первоначально разместив исходные данные в таблице 1.

Таблица 1.

Содержание питательных веществ в продукции

Экономико-математическая модель примет вид:

                                                       (1)

                                                       (2)
 

Целевую функцию (1) и систему ограничений неравенств можно записать через ∑ (сумму):

                                                                              (3)

                                                                  (4)

В задаче составления диеты (рациона, кормовой смеси) могут использоваться ограничения не только по необходимому минимуму необходимых веществ, но и по минимальному весу смеси.

Например, организация может купить n видов сырья и приготавливать различные виды смесей. Каждое сырье содержит разное количество необходимых веществ для смеси. Смесь должна удовлетворять минимальным требованиям полезности. Необходимо определить количество каждого j-го вида сырья, образующего смесь минимальной стоимости при соблюдении требований к общему расходу смеси и её питательность.

Экономико-математическая модель задачи будет иметь вид:

 ,

при ограничениях:

·     на общий расход смеси: ;

·     на питательность смеси: ;

·     на не отрицательность переменных: ;

где: х_j – количество j-го сырья в смеси; n – количество видов сырья; m – количество питательных веществ;

a_ij– количество i-го питательного вещества, содержащегося в единице j-го вида сырья;

b₁ – минимальное количество i-го питательного вещества, содержащегося в единице смеси;

c_j – стоимость единицы сырья j;

q – минимальный общий вид смеси [2].

Составление экономико-математической модели и решение задачи о диете.

Для составления экономико-математической формулировки задачи о диете необходимо ввести следующие данные: P₁ и P₂ – виды продукции (белые грибы, облепиха), B₁, B₂, B₃, B₄ (белки, жиры, углеводы, витамины) – содержащиеся в них питательные вещества. Содержание питательных веществ в единице продукции и необходимый минимум питательных веществ приведены в таблице 2.

Таблица 2.

Содержание питательных веществ в продукции

Стоимость единицы продукции P₁ и P₂ соответственно равна 4 и 3 у.е. Необходимо рассчитать дневной рацион, удовлетворяющий необходимому минимуму питательных веществ при минимальных затратах.

Решение. х₁ и х₂ – количество продукции P₁ и P₂, входящей в дневной рацион. Общая стоимость рациона составит (у.е.):

                                                                                  (5)

Необходимо составить систему ограничений с учетом необходимого минимума питательных веществ. Рацион включает в себя:  единиц необходимого питательного вещества B₁ (белков),  единиц необходимого питательного вещества B₂ (жиров),  единиц необходимого питательного вещества B₃ (углеводов) и  единиц необходимого питательного вещества B₄ (витаминов). Так как содержание необходимых питательных веществ B₁, B₂, B₃, B₄ в рационе должно быть не менее 10, 8, 9, 11 единиц, соответственно, то система ограничений неравенств будет следующая:

                                                                            (6)

Экономико-математическая модель задачи будет состоять в следующем: составить дневной рацион , при котором функция (5) принимает минимальное значение и рацион должен удовлетворять системе ограничений (6).

Решение данной задачи возможно при помощи графического метода (т.к. всего 2 переменные).

;         ;

Для решения необходимо построить график каждого уравнения. Для этого берется произвольное значение х₂ и подставляется в уравнение и находится х₁. Далее полученные координаты соединяются прямой. Например, для уравнения ,  будет равен 0. ,  будет равен 5. И получаем точки (0;10) (5;0) и соединяем их прямой. Для того чтобы узнать необходимую полуплоскость, подставляется в неравенство точка (0;0). И так для каждого уравнения, в итоге получается графическая система неравенств (Рисунок 1).

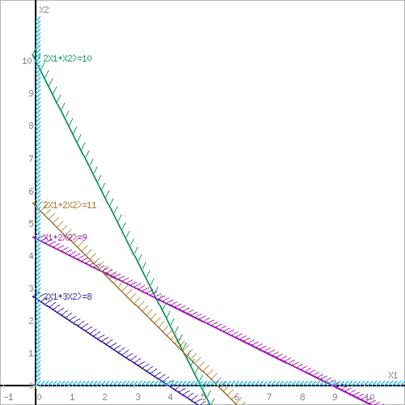
Рисунок 1. Графическая система неравенств

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Границы области многоугольника решений обозначены на рисунке 2.

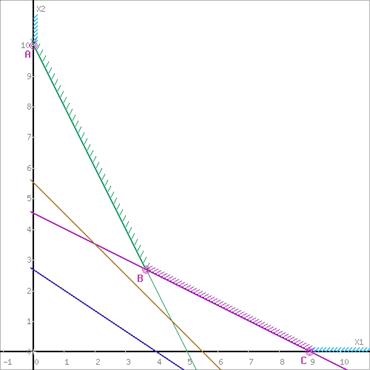
Рисунок 2. Границы области допустимых решений

Далее необходимо построение прямой, отвечающей значению функции . Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(Х). Начало вектора – точка (0;0), конец – точка (4; 3). Необходимо двигать линию уровня, перпендикулярную вектору-градиенту, параллельным образом по направлению вектора. Так как значение функции стремится к минимуму, то необходимо двигать прямую до первого касания обозначенной области. На рисунке 3 эта прямая обозначена пунктирной линией.

Прямая  пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

;

;

;         

Решив систему уравнений, становится известно, что: 

Откуда возможно найти минимальное значение целевой функции:

(Рисунок 3)

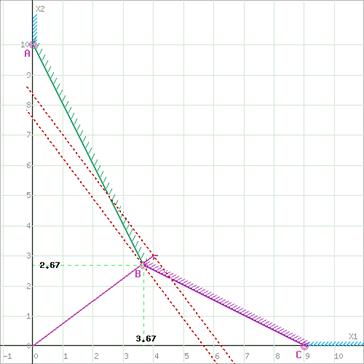
Рисунок 3. График решения

Ответ: необходимо 400 грамм первого продукта (белых грибов) и 300 грамм второго продукта (облепихи); минимальная цена дневного рациона будет 23 у.е.

Применение математической модели решения задач о диете значительно облегчает процесс создания определенного рациона питания (диеты), а также позволяет экономить средства.