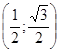ОПТИМИЗАЦИЯ ПРИБЫЛИ ТОРГОВОЙ ФИРМЫ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Секция: 11. Экономика

XIX Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
ОПТИМИЗАЦИЯ ПРИБЫЛИ ТОРГОВОЙ ФИРМЫ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
В курс программы обучения студентов по направлению «Экономика» помимо экономических дисциплин, включено множество других, в частности, математика и ее разделы: математический анализ, линейная алгебра и т. д. Это является следствием того, что экономика и математика как науки идут неразрывно друг с другом и взаимно дополняют друг друга. Множество математических законов и теорем применяются в экономической науке, например, теоремы о производной, которым посвящена данная исследовательская работа.
Проанализировав экономический смысл производной, нетрудно заметить, что многие, в том числе базовые законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем.
Рассмотрим теорему: если дифференцируемая на промежутке X функция y= f(x) достигает наибольшего или наименьшего значения во внутренней точке x0 этого промежутка, то производная функции в этой точке равна нулю, то есть f’(x0) = 0. Какова ее экономическая интерпретация?
В рыночной экономике в условиях совершенной конкуренции, которая является идеальной экономической моделью, оптимальный объем выпуска товара производителем достигается при равенстве предельных издержек и предельного дохода.
Это значит, что объем выпуска Qo оптимален для производителя, если ![]() , где MC — предельные издержки, а MR — предельный доход.
, где MC — предельные издержки, а MR — предельный доход.
Примем функцию прибыли за П(Q). Тогда ![]() , где R — прибыль, а C — общие издержки производства.
, где R — прибыль, а C — общие издержки производства.
Несомненно, оптимальный объем производства достигается при максимизации прибыли, то есть в таком значении Qo, при котором функция П(Q) имеет экстремум (максимум). По теореме Ферма в этой точке ![]() . Но
. Но ![]() , поэтому
, поэтому ![]() , следовательно,
, следовательно, ![]() .
.
Для максимизации дохода прибегают к снижению издержек производства товара до минимальных. В результате, оптимальный объем выпуска продукции достигается при равенстве средних и предельных издержек.
Это условие является следствием сформулированной выше теоремы. Средние издержки AC(Q) определяются как ![]() , т. е. издержки производства всей партии товара, деленные
, т. е. издержки производства всей партии товара, деленные
на количество единиц произведенного товара. Эта величина достигает своего минимума в критической точке функции y=AC(Q), т.е. при условии ![]() ,
,
откуда ![]() или
или 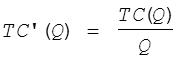 , т. е. MC(Q)=AC(Q).
, т. е. MC(Q)=AC(Q).
Понятие «выпуклость функции» также интерпретируется в экономической теории.
Один из самых известных экономических законов — закон убывающей доходности — читается так: «с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т. д.), с некоторого момента убывает».
Другими словами, величина ![]() , где Dy — приращение выпуска продукции, а Dx — приращение ресурса, уменьшается при увеличении x. Итак, закон убывающей доходности формулируется как функция y= f(x), выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
, где Dy — приращение выпуска продукции, а Dx — приращение ресурса, уменьшается при увеличении x. Итак, закон убывающей доходности формулируется как функция y= f(x), выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
Данный подход может применяться на практике для определения объема выпуска продукции с наименьшими издержками.
В качестве примера рассмотрим такую ситуацию на рынке. Предприятие, занимающееся лесозаготовкой, в день производит Х тонн древесины в неделю. По договору оно должно ежедневно поставлять целлюлозно-бумажному комбинату не менее 20 т древесины. Производственные мощности завода таковы, что заготовка древесины не может превышать 90 т в день.
Для определения такого объема производства, при котором удельные затраты будут наименьшими, проведем исследование функции затрат предприятия.
![]() .
.
Удельные затраты составят ![]() .
.
Таким образом, требуется найти наименьшее значение функции
![]() на отрезке [20; 90].
на отрезке [20; 90].
Используя необходимый признак существования экстремума, получаем, что ![]() является стационарной (критической) точкой функции. Сравним значения функции в концах данного отрезка и в критической точке.
является стационарной (критической) точкой функции. Сравним значения функции в концах данного отрезка и в критической точке.
![]() .
.
Исходя из произведенных расчетов, выпуская 90 тонн древесины в день, предприятие минимизирует издержки, а это значит, что при выпуске комбинату необходимо задействовать все ресурсы и усовершенствовать технологию производства, т. к. в дальнейшем свое влияние будет оказывать закон убывающей доходности.
Максимальная прибыль предприятия достигается в случае сочетания минимальных издержек при выпуске определенного объема продукции и оптимальной цены ее реализации. Неограниченное повышение цены не выгодно для потребителя, поэтому производителю следует определить максимальную цену, при которой можно реализовать максимально большой объем выпуска продукции.
Пусть выручка торговой фирмы вычисляется по формуле: ![]() , где p — цена, тогда
, где p — цена, тогда ![]() . Проведем исследования функции U(p) с помощью производной.
. Проведем исследования функции U(p) с помощью производной.
Имеем ![]() . Производная функции U(p) положительна при p<0,5 и отрицательна при p>0,5, функция возрастает при p<0,5 и убывает при p>0,5, то есть с ростом цены доход фирмы вначале увеличивается, при p=0,5 достигает наибольшего значения
. Производная функции U(p) положительна при p<0,5 и отрицательна при p>0,5, функция возрастает при p<0,5 и убывает при p>0,5, то есть с ростом цены доход фирмы вначале увеличивается, при p=0,5 достигает наибольшего значения ![]() , но дальнейшее увеличение цены приводит к сокращению дохода.
, но дальнейшее увеличение цены приводит к сокращению дохода.
Темп изменения выручки определим с помощью второй производной.
![]()
При ![]()
![]() , при
, при ![]()
![]() , т. е. темп изменения выручки
, т. е. темп изменения выручки
положительный и отрицательный соответственно.
На интервале (0;0,5) функция возрастает всё медленнее, то есть дальнейшее повышение цены становится не выгодным. Сначала выручка убывает с отрицательным темпом для ![]() , а затем, темп убывания становится положительным и для p>0,9
, а затем, темп убывания становится положительным и для p>0,9
выручка убывает все быстрее и в итоге стремится к нулю при бесконечном увеличении цены.
Итак, составим таблицу и построим график данной функции.
Таблица 1.
Значение производных первого и второго порядка функции выручки фирмы и характеристика функции
p |
(0, 0,5) |
0,5 |
|
|
|
U'(p) |
+ |
0 |
- |
-0,47 |
- |
U''(p) |
- |
|
- |
0 |
+ |
U (p) |
возрастающая выпуклая |
0,3 max |
убывающая выпуклая |
0,2 точка перегиба |
убывающая вогнутая |
Таким образом, можно сделать вывод:
На промежутке (0;0,5) функция возрастает все медленнее.
Соответствующая часть графика выпукла. Выше уже отмечалось, что дальнейшее повышение цены не выгодно. Сначала выручка убывает с отрицательным темпом (при ![]() ), а затем темп убывания U(p) становится положительным. Для р>0,9 доход
), а затем темп убывания U(p) становится положительным. Для р>0,9 доход
убывает все быстрее и стремится к нулю при бесконечном увеличении цены. На промежутке 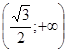 функция U(p) вогнута. В точке
функция U(p) вогнута. В точке 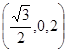 график перегибается (рис. 1):
график перегибается (рис. 1):
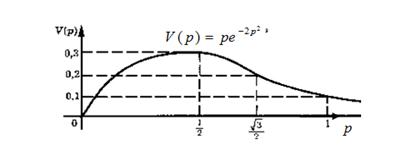
Рисунок 1. График зависимости выручки торговой фирмы от цены
Таким образом, в данной работе был проанализирован экономический смысл производной, а также найдено ее практическое применение к определенному типу экономических ситуаций. Теоремы о производной используются в экономике непосредственно и являются важнейшим элементом при определении объема выпускаемой продукции и максимизации прибыли фирмы.
Список литературы:
1. А.М. Иванов, А.В. Аникин, А.В. Бухвалов. Суммарные, средние и предельные величины // Экономическая школа. СПб, 1991. Т. 1, вып. 1 — С. 174—179.
2. Сборник задач по математике: учебное пособие / под редакцией С.И. Макарова, М.В. Мищенко. — Самара: Издательство Самарский государственный экономический университет, 2007 г. — 356 с.