ВЫЧИСЛЕНИЕ ЭКОНОМИЧЕСКОЙ ПРИБЫЛИ ПРИ ПОМОЩИ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Секция: 11. Экономика

VII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
ВЫЧИСЛЕНИЕ ЭКОНОМИЧЕСКОЙ ПРИБЫЛИ ПРИ ПОМОЩИ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Неразрывная связь между экономикой и математикой давно стала очевидна человечеству, ведь ведение хозяйства подразумевает множество математических вычислений. И чем глубже исследования в области математики, в частности математического анализа, тем более точные данные возможно получить в экономической сфере.
Применение определенного интеграла в экономике давно перестало считаться нововведением. Но, если говорить о необходимых расчетах в условиях работы различных компаний, предприятий, можно рассматривать все расчеты с точки зрения программирования. Поэтому применение интегральных уравнений для решения экономических задач будет рассматриваться в качестве необходимого материала для учащихся средних и высших учебных учреждений.
Весьма часто практическое применение определенного интеграла ограничивается лишь вычислением площадей фигур, в экономических классах школ и в экономических вузах — решением простейших экономических задач. Тогда как интегральное исчисление помогает реализовать 2 направления: усвоению экономического материала и более системному и фундаментальному пониманию интеграла.
В различных источниках литературы можно встретить примеры использования интегрального вычисления в экономике, но чаще всего авторы ограничивались начальными темами курса микроэкономики (спрос и предложение, вычисление потребительского излишка и т. п.)
Для начала можно остановиться на вычислении суммарной экономической прибыли фирмы в долгосрочном периоде. Для этого понадобится ввести ряд экономических терминов, понятий и обозначений.
P (price) — цена данного товара, выпускаемого фирмой;
Q (quantity) — объем товара, выпускаемый производителем;
TR (total revenue) — валовой доход, т. е. весь совокупный доход фирмы от продажи конкретного количества товара за определенную цену;
TC (total costs) — валовые издержки: совокупность всех расходов фирмы на выпуск конкретного объема товара;
Основным мотивом и движущей системой деятельности фирмы является прибыль. Она представляет собой разницу между совокупной выручкой и совокупными издержками фирмы. Она обозначается P(profit):
P=TR-TC
Рассмотрим совокупную экономическую прибыль фирмы-монополиста. Графики функций TR и TC представляют собой параболы, ветви которых соответственно направлены вниз и вверх.
Функции задаются переменными P(ось Y) и Q(ось Х)
TR=-x2+8x-7 и TC=x2-8x+17. Координаты точек пересечения графиков функций TR и TC соответственно отображают объем выпускаемой продукции, при котором фирма-производитель будет иметь только нормальную прибыль, при которой TR-TC=0. Нас интересуют расчеты экономической прибыли в длительном периоде, т.к. предприятие в течение времени t увеличивает объем выпуска Q на ΔQ.
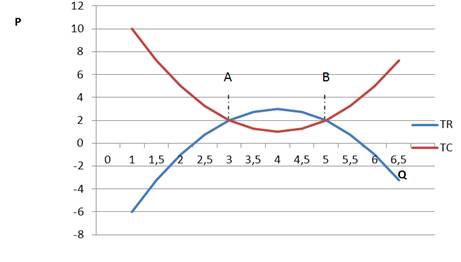
Диаграмма 1. Достижение экономической прибыли путем сравнения
TR и TC( предельного дохода и предельных издержек)
При помощи интегрального уравнения достаточно легко получить искомое значение. Пределами интегрирования являются значения Q1 и Q2, где TR=TC.
1) x2-8x+17=-x2+8x-13 а значит x1= QА=3и x2=QВ= 5
Геометрически зона экономической прибыли представляет собой площадь пересечения графиков заданных функций. Таким образом, разница определенных интегралов функций TR и TC, т. е. разности площадей криволинейных трапеций является искомым значением площади (необходимые и достаточные условия выполняются для обеих функций) [3, с. 471].
![]() -
-![]()
Так как разность интегралов равна разности подынтегральных выражений, получим:
![]() =
=
= ![]() =
=![]() (
(![]() +4
+4![]() -15x)
-15x) ![]() =
=
=-2(![]() +200-75)+2(9+36-45)=
+200-75)+2(9+36-45)=![]() =-166
=-166![]()
Монополист действует на рынке в отсутствие соперников. Поэтому в противоположность совершенно конкурентному предприятию, чья экономическая прибыль в длительном периоде (благодаря увеличению числа предприятий) сводится к нулю, монополист может получать положительную экономическую прибыль и в длительном периоде. С другой стороны, как и в случае совершенной конкуренции, экономическая прибыль монополиста в длительном периоде не может быть отрицательной [1, с. 83]. Следовательно,
P=|-166![]() |=166
|=166![]()
Подобные расчеты производятся довольно быстро, однако в учебных заведениях редко производятся. Между тем, данные задачи несут междисциплинарный характер и помогают освоению материала как в области экономики, так и в области математического анализа. Нельзя не отметить непосредственно прикладной характер определенного интеграла: имея данные фирмы об объемах производства, производственных мощностях, расходах и доходах, становится возможным вычисление прибыли за конкретный период.
Расчет экономической прибыли возможен при анализе иных функций: как при сравнении объема максимизирующей прибыли, возможно сравнение как TC и TR в длительном периоде, так и MR и TR в короткосрочном.
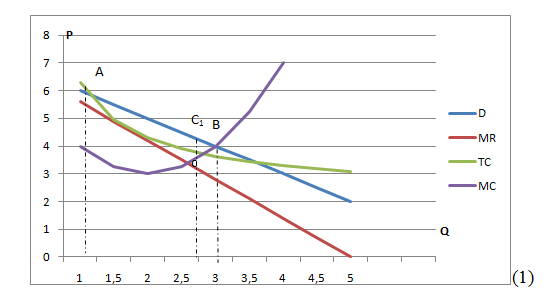
Диаграмма 2.Достижение экономической прибыли путем сравнения
MR и MC(предельного дохода и предельных издержек)
где: MR-предельный доход MR=(TR)’. Доход, получаемый с каждой дополнительной единицы товара. MR= -1,4q+5
MC-предельные издержки. Издержки фирмы от производства каждой дополнительной единицы товара. VC=(TC)’ ; ТС=![]() +2,3 ; МС=(q-2)2+3
+2,3 ; МС=(q-2)2+3
Лини МС ниже D, т.к. в условиях монополии. Это обусловлено тем,чтопродажа дополнительной единицы продукции требует от монополиста снижения цен на нее.
D= - q+7
График ТС лежит ниже кривой спроса(D). При ТС<D возможны доход и прибыль фирмы. Однако площадь, получаемая при пересечении данных прямых не соответствует площади, отображающей зоны экономической прибыли. Необходимо так же учесть предельные издержки МС. Таким образом, площадь треугольной фигуры АВС является графическим отображением зоны экономической прибыли.
Для расчета потребуется разбить фигуру на части, т. к. ![]() имеют совпадающие сегменты, а потому пределами интегрирования будут являться значения Qa, Qb, Qc.(Графики функций МС и ТС пересекаются в т.С)
имеют совпадающие сегменты, а потому пределами интегрирования будут являться значения Qa, Qb, Qc.(Графики функций МС и ТС пересекаются в т.С)
1) QA; TC=D ; ![]() +2,3=- q+7 ; q~1 =QA
+2,3=- q+7 ; q~1 =QA
QB; MC=D; (q-2)2+3=- q+7 ; q=3[1]
QC; TC=MC; ![]() +2,3=(q-2)2+3; q~2,8
+2,3=(q-2)2+3; q~2,8
2)![]() =
=
= -(![]() -4,7q+4
-4,7q+4![]() )
) ![]() =2,9
=2,9
3) ![]() -((q-2)2+3))
-((q-2)2+3))![]() =
=
=-(![]() -11,7q -
-11,7q -![]() )
)![]() =1,1
=1,1
4) S1+S2=2,9+1,1=4=P
Для расчетов использовались более легкие функции, чем те, которые встречаются на практике. В данной работе они используются в упрощенном виде, а для удобства подсчета округлены. Однако, алгоритм вычислений соблюдается полностью.
Список литературы:
- Гальперин В.М., Игнатьев С.В. Микроэкономика в 2 томах. Учеб. пособие для вузов — СПб.: 1999. — 494 с.
- Математика для экономистов Задачник,учебно-практическое пособие под редакцией С.И. Макарова и М.В. Мищенко. — М-Конус. 2008 — 360 с.
- Математический анализ начальный курс В.А. Ильин, В.А. Садовничий — М.: изд. МГУ 1985





