ОЦЕНКА ПАРАМЕТРОВ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ КОББА-ДУГЛАСА В ТРАНСПОРТНО-ЛОГИСТИЧЕСКОМ СЕКТОРЕ РЕСПУБЛИКИ БЕЛАРУСЬ
Секция: Экономика

LVIII Студенческая международная научно-практическая конференция «Общественные и экономические науки. Студенческий научный форум»
ОЦЕНКА ПАРАМЕТРОВ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ КОББА-ДУГЛАСА В ТРАНСПОРТНО-ЛОГИСТИЧЕСКОМ СЕКТОРЕ РЕСПУБЛИКИ БЕЛАРУСЬ
Производственные функции – это достаточно широко известный инструмент анализа зависимости между затратами и результатами производства как на микро-, так и на макроуровне. Безусловно, самая известная производственная функция носит название по именам её авторов – Ч. Кобба и П. Дугласа [5].
Функциональная форма Кобба-Дугласа широко используется в экономике. Она была предложена Кнутом Виксель, и проверена на статистических данных Чарльзом Коббом и Полом Дугласом в 1928 году. В 1928 году Чарльз Кобб и Пол Дуглас опубликовали исследование, в котором они смоделировали рост американской экономики в период 1899 г. – 1922 г. Они брали два фактора, которые по их мнению влияли на общий объем производства. В то время, как многие другие факторы влияли на экономические показатели, их модель оказалась удивительно точной. Функция, которую они использовали для моделирования производства, была вида [3]:
![]() (1)
(1)
где Q – общий объем производства (денежная стоимость всех товаров, произведенных в течение года);
L – рабочая сила (общее количество рабочих за год);
K – входной капитал (денежная стоимость всех машин, оборудования и зданий);
α – число масштаба;
β₁ и β₂ являются выходной эластичностью труда и капитала, соответственно.
Целью данной работы является построение производственной функции Кобба-Дугласа и оценка ее параметров. Для выполнения поставленной задачи и проведения анализа будут использованы экономические показатели тридцати различных компаний логистического сектора Республики Беларусь.
В качестве данных выступают следующие показатели: выпуск Q, трудозатраты L и капиталовложения K.
Все данные представлены в таблице 1.
Таблица 1.
Показатели состава капитала логистических операторов за 2021 г., тыс. руб.
|
Фирма |
Q |
L |
K |
Фирма |
Q |
L |
K |
|
1 |
6502 |
7101 |
4320 |
16 |
6990 |
7120 |
5990 |
|
2 |
6334 |
6988 |
5432 |
17 |
7120 |
7149 |
6984 |
|
3 |
6128 |
6559 |
6001 |
18 |
6950 |
6990 |
5990 |
|
4 |
6150 |
7009 |
5866 |
19 |
6430 |
6440 |
5887 |
|
5 |
5805 |
6020 |
5229 |
20 |
7350 |
7559 |
7114 |
|
6 |
6669 |
6129 |
5448 |
21 |
7100 |
7231 |
6588 |
|
7 |
6734 |
7389 |
6694 |
22 |
7080 |
7109 |
6998 |
|
8 |
6955 |
7349 |
6120 |
23 |
7014 |
7020 |
6412 |
|
9 |
7280 |
7600 |
6899 |
24 |
6850 |
6950 |
6099 |
|
10 |
7432 |
7559 |
7220 |
25 |
6349 |
6680 |
6209 |
|
11 |
5989 |
6200 |
5832 |
26 |
6432 |
6604 |
6113 |
|
12 |
6902 |
7080 |
6644 |
27 |
6453 |
6984 |
6160 |
|
13 |
6120 |
5698 |
6488 |
28 |
6884 |
7136 |
6554 |
|
14 |
6220 |
6409 |
5698 |
29 |
7003 |
7436 |
6889 |
|
15 |
5990 |
6320 |
5760 |
30 |
6980 |
7098 |
6901 |
На основании имеющихся данных по логистическим компаниям проведем анализ эконометрических моделей и выявим зависимость между выпуском Q, с одной стороны, и трудозатратами L и капиталовложениями K, с другой стороны.
На первом этапе проводимого анализа построим эконометрическую модель, используя в качестве данных выпуск Q, трудозатраты L и капиталовложения K. Для решения поставленной задачи и выполнения расчётов был использован MS EXCEL (пакет «Анализ данных»). После выполнения несложных операций были получены следующие результаты, изображенные на рисунке 1.

Рисунок 1. Вывод итогов
Таким образом, на основе анализа соотношений была получена модель следующего вида: ![]() . На основании полученных результатов можно сделать вывод, что коэффициент а0 значим на уровне надежности 0,9, но данный коэффициент не значим на уровнях надежности 0,95 и 0,99. Коэффициент а1 значим на всех уровнях надежности. Коэффициент а2 также значим на всех уровнях надежности.
. На основании полученных результатов можно сделать вывод, что коэффициент а0 значим на уровне надежности 0,9, но данный коэффициент не значим на уровнях надежности 0,95 и 0,99. Коэффициент а1 значим на всех уровнях надежности. Коэффициент а2 также значим на всех уровнях надежности.
F-расчетное равно 40,605. R-квадрат значим, так как F-расчетное, равное 40,605, больше F-табличного для всех уровней надежности. Исходя из этого, уравнение регрессии следует признать адекватным.
Множественный коэффициент корреляции R, равный 0,866, свидетельствует о тесной связи между признаками. Множественный коэффициент детерминации R-квадрат, равный 0,75, показывает, что 75% вариации величины Q происходит за счёт вариации величин L и K, а остальные 25% вариации величины lnQ происходит под влиянием прочих неучтенных факторов.
На втором этапе проведенного исследования оценим по представленным данным логистических компаний Республики Беларусь производственную функцию Кобба-Дугласа.
Перейдем к решению данной задачи. Для начала прологарифмируем уравнение ![]() . Таким образом, получим следующее:
. Таким образом, получим следующее:
 (2)
(2)
![]() (3)
(3)
Для решения поставленной задачи и расчетов параметров функции Кобба-Дугласа также воспользуемся программой MS EXCEL [2].
В MS EXCEL было рассчитано три дополнительных показателя, которые отражали следующие значения: “lnQ”, “lnL” и “lnK”, где “lnQ” – логарифм данных из столбца “Q”, “lnL” – логарифм данных из столбца “L” и “lnK” – логарифм данных из столбца “K”. После этого построили модель по полученным расчетным показателям. В итоге были получены следующие результаты, изображенные на рисунке 2.
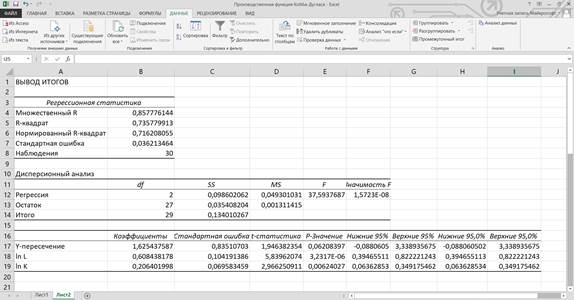
Рисунок 2. Вывод итогов
На основе полученных результатов расчёта, представленных на рисунке 2, делаем вывод о том, что ![]()
Однако над коэффициентом ![]() проводим еще одну операцию, так как
проводим еще одну операцию, так как ![]()
Таким образом, после проведения анализа и определения коэффициентов уравнения, сформируем производственную функцию Кобба-Дугласа. Данная функция примет следующий вид:
![]() (4)
(4)
Коэффициент детерминации, который также называется R-квадрат, равен 0,7358.
Нормированный (скорректированный) коэффициент детерминации из ячейки равен 0,7162.
Множественный коэффициент корреляции равен 0,8578.
По значению R-квадрат, равному 0,7358, можно сделать вывод о том, что 73,58% вариации величины lnQ происходит за счёт вариации величин lnL и lnK, а остальные 26,42% вариации величины lnQ происходит под влиянием прочих неучтенных факторов. Помимо этого, узнав значение критерия Фишера, равное 37,59, можно сделать вывод о значимости R-квадрат. Модель является адекватной, так как значение R-квадрат больше 0,7 [1].
Обратив внимание на построенную функцию, можно заметить, что β₁ + β₂ < 1. Исходя из этого, можно сделать вывод о том, что имеет место убывающая отдача от масштаба.
Найдём выборочный коэффициент корреляции между lnL и lnK. В результате вычислений получили выборочный коэффициент корреляции, равный 0,4642. Интерпретируем полученное значение согласно таблице 2.
Таблица 2.
Анализ силы связи между переменными – Источник[2]
|
Значение |
Интерпретация |
|
от 0 до 0,3 |
очень слабая |
|
от 0,3 до 0,5 |
слабая |
|
от 0,5 до 0,7 |
средняя |
|
от 0,7 до 0,9 |
высокая |
|
от 0,9 до 1 |
очень высокая |
Данное значение находится в диапазоне от 0,3 до 0,5. Следовательно, глядя на таблицу анализа силы связи между переменными (таблица 2), можно сделать вывод о том, что величина рассчитанного в данной работе коэффициента корреляции указывает на слабую мультиколлинеарность факторов lnL и lnK.
На третьем этапе проведенного исследования исключим фактор трудозатраты L из нашей модели и проведем регрессию lnQ только на lnK. В выводе итогов получим следующие результаты, изображенные на рисунке 3.

Рисунок 3. Вывод итогов
Получили следующие коэффициенты:
![]()
Таким образом, после проведения ещё одного анализа и определения коэффициентов, сформируем производственную функцию Кобба-Дугласа. В этот раз функция примет следующий вид:
![]() (5)
(5)
Коэффициент детерминации равен 0,4021.
Нормированный (скорректированный) коэффициент детерминации равен 0,3807.
Множественный коэффициент корреляции равен 0,6341.
Таким образом, можно легко заметить, что коэффициенты детерминации и корреляции значительно снизились для уравнения (5) по сравнению с уравнением (4). То есть качество уравнения (5) значительно хуже, нежели уравнения (4). Исходя из этого следует сказать, что основное влияние на выпуск Q оказывают трудозатраты L, ввиду того, что их исключение в значительной степени снижает качество уравнения регрессии. Скорее всего, в нашей модели присутствует мультиколлинеарность [4].
На четвертом этапе предложим решение проблемы мультиколлинеарности, возникающей в модели. Подставляя β₂ = 1 - β₁ в уравнение ![]() после элементарных преобразований получим:
после элементарных преобразований получим:
 (6)
(6)
Оценив эту регрессию, получим следующие результаты, изображенные на рисунке 4.

Рисунок 4. Вывод итогов
Качество регрессии хорошее. Таким образом, введение ограничения β₁ + β₂ = 1 позволило в данном случае решить проблему мультиколлинеарности. Если говорить в целом о всей работе, то в результате проведения регрессионных анализов можно отметить, что наибольшее влияние на выпуск Q оказывают именно трудозатраты L, ввиду того, что их исключение в значительной степени снижает качество уравнения регрессии. Наиболее хорошо специфицированной моделью является последняя модель, в которой было осуществлено введение ограничения β₁ + β₂ = 1 для решения проблемы мультиколлинеарности.
C помощью построенной модели было определена сила влияния факторов трудозатраты L и капиталовложения K на выпуск Q. Благодаря построенной функции Кобба-Дугласа, логистические операторы, используя данную модель, имеют возможность осуществлять построение прогноза для выпуска Q.





