Численное моделирование высокоскоростного пробития плиты из композиционного материала ударником
Конференция: XLVI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Технические науки

XLVI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Численное моделирование высокоскоростного пробития плиты из композиционного материала ударником
Явление высокоскоростного взаимодействия твердых тел находит широкое применение в технике, промышленности, военном деле. При рассмотрении таких процессов главной задачей является изучение степени разрушения и фрагментации взаимодействующих твердых тел на основе расчета и анализа напряженно-деформированного состояния. Поэтому исследование подобных процессов является весьма актуальной задачей. Изучение процессов проникновения и разрушения, как правило, выполняется, вследствие их сложности и взаимосвязанности, численными методами, методом конечных элементов и методом гладких (сглаженных) частиц.
Предметом исследования этой работы являются процессы деформирования и разрушения твердых тел при высокоскоростном взаимодействии на основе рассмотрения системы «ударник-плита».
Рассматривается задача динамического взаимодействия твердого движущегося тела (ударника ÆD=5,6 мм, L=56 мм) при различных линейных и вращательных скоростях с неподвижной преградой (плитой из материала - триплекса), их деформация и разрушение в трехмерной постановке.
Общий вид геометрии взаимодействующих тел представлен на рисунке 1.
Расчётная модель представляет собой плиту в виде прозрачной брони «триплекс». Данный вид брони имеет два слоя кварцевого стекла скреплённых тонкой полимерной плёнкой. Такой вариант остекления применяется в качестве защиты для окон автомобилей специального назначения, самолетов и вертолетов, окон наблюдения на кораблях, иллюминаторов подводных лодок и т. д.
Совместная толщина рассматриваемой плиты равна 10 мм, при этом толщина плёнки составляет всего 0,4 мм. Ударник представляет собой цилиндр с полусферическим наконечником (ÆD=5 мм, L=12 мм) изготовлен из стали 4340. Плита выполнена из двух кварцевых стекол, соединенных пленкой EVA. Механические свойства материалов представлены в таблице 1.

Рисунок 1. Угол встречи ![]()
Таблица 1.
Механические свойства материалов
|
|
Сталь 4340 |
Кварцевое стекло |
Пленка EVA |
Ед. измерения |
|
ρ |
7830 |
2530 |
955 |
кг/м3 |
|
G |
81,8 |
30,4 |
- |
ГПа |
|
|
792 |
- |
- |
МПа |
|
|
1520 |
- |
- |
K |
|
E |
- |
- |
80 |
МПа |
|
µ |
- |
- |
0,4 |
- |
|
К |
- |
45,4 |
- |
ГПа |
ρ – плотность;
E – модуль упругости Юнга;
µ – коэффициент Пуассона;
G – модуль упругости второго рода;
K – объёмный модуль упругости;
![]() – напряжение текучести при сжатии;
– напряжение текучести при сжатии;
![]() – температура начала плавления.
– температура начала плавления.
Рассматриваемые скорости встречи ударника с плитой: 280 м/c, 450 м/c, 800 м/с. Векторы скоростей и условия закрепления, используемые в модели представлены на рисунке 2. Угловая скорость вращения определяется по формуле:
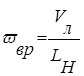 (1)
(1)
где: ![]() – линейная скорость;
– линейная скорость;
![]() – шаг нарезов в канале ствола.
– шаг нарезов в канале ствола.
Шаг нарезов в канале ствола был выбран 240 мм. Получившиеся скорости вращения составили vвр=6283 рад/c, 11781 рад/c, 15708 рад/c соответственно.
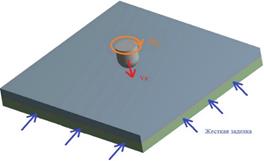
Рисунок 2. Скорости, действующие на ударник, закрепление плиты
Данная задача в силу сложной геометрической формы деталей и самого явления не решаема аналитическими методами, поэтому используется численный метод конечных элементов.
Основное уравнение МКЭ традиционно записывается в виде:
![]() (2)
(2)
где: ![]() – матрица жёсткости;
– матрица жёсткости;
![]() – вектор перемещений;
– вектор перемещений;
![]() – вектор усилий.
– вектор усилий.
Так как задача динамическая, уравнение принимает следующий вид:
![]() (3)
(3)
где: ![]() – матрица масс;
– матрица масс;
![]() – вектор узловых ускорений;
– вектор узловых ускорений;
![]() – матрица демпфирования;
– матрица демпфирования;
![]() – вектор узловых скоростей.
– вектор узловых скоростей.
Строго говоря, все параметры этого уравнения меняются во времени.
Вычисления проводились с помощью расчётного модуля Explicit Dynamics программы Ansys Workbench. Уравнения с частными производными, решаемые в Explicit Dynamics, выражают сохранение массы, импульса и энергии в лагранжевых координатах. Они, вместе с моделью материала и набором начальных и граничных условий, определяют полное решение задачи.
Для лагранжевых формулировок, доступных в настоящее время в системе Explicit Dynamics, сетка перемещается и изменяется с помощью процедур, которые она использует, а сохранение массы выполняется автоматически. Плотность в любое время определяется по текущему объёму и начальным величинам скорости и массы:
![]() (4)
(4)
Уравнения в частных производных, выражающие сохранение импульса, связаны с ускорением и компонентами ![]() тензора напряжений:
тензора напряжений:
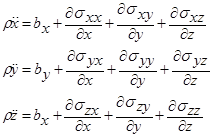 (5)
(5)
Сохранение энергии выражается через:
![]() (6)
(6)
где: ![]() - ускорение;
- ускорение;
![]() - компоненты тензора напряжений, считающиеся постоянными на шаге времени;
- компоненты тензора напряжений, считающиеся постоянными на шаге времени;
![]() - компоненты скорости деформаций.
- компоненты скорости деформаций.
Эти уравнения решаются явно для каждого элемента модели, основываясь на входных значениях в конце предыдущего шага времени. Для обеспечения стабильности и точности решения выбираются небольшие временные приращения (шаги по времени).
При расчетах в Explicit Dynamics были использованы конечные элементы типа Solid 164, предназначенные для трехмерного моделирования сплошных структур. Эти элементы определяются восемью узлами со всеми степенями свободы в каждом узле: перемещением, скоростью и ускорением по направлениям X, Y и Z [4].
Вид подобных элементов показан на рисунке 3.
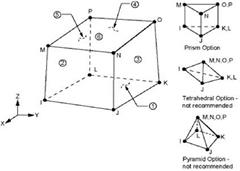
Рисунок 3. Схема конечного восьми узлового элемента
Характер поля распределения напряжений в пространстве плиты для начальной линейной скорости ударника 280 м/с и скорости вращения 6283 рад/c представлен на рисунке 4



Рисунок 4. Эквивалентные напряжения в плите, при разной глубине проникновения ударника
Пленка, склеивающая два кварцевых стек ла является неким изолятором в связи с чем, в начальный момент столкновения, можно наблюдать, как волна напряжения, в первые этапы проникновенияударника, не распространяется на второй слой стекла.

Рисунок 5. Эквивалентные напряжения в ударнике

Рисунок 6. Форма разрушения плиты
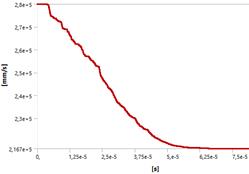
Рисунок 7. Линейная скорость ударника в процессе контакта

Рисунок 8. Температура материала поверхности трения ударника
В решаемой задаче формой разрушения плиты является отверстие, полученное в результате откола элементов. Данный вид разрушения вызван появлением разрушающего напряжения в частицах стекла. Максимальную деформацию сдвига (1,6 мм), в этом расчёте и всех приведённых ниже, испытывает пленка, склеивающая стекла.
При начальной линейной скорости ударника 450 м/с и скорости вращения 11781 рад/c:

Рисунок 9. Пластические деформации в ударнике после пробития и форма разрушения плиты
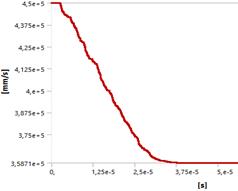
Рисунок 10. Линейная скорость ударника в процессе контакта

Рисунок 11. Температура сферической поверхности ударника
При начальной линейной скорости ударника 800 м/с и скорости вращения 15708 рад/c:
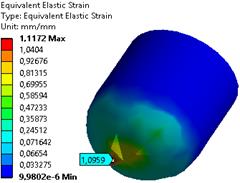

Рисунок 12. Пластические деформации в ударнике после пробития и форма разрушения плиты

Рисунок 13. Линейная скорость ударника в процессе контакта

Рисунок 14. Температура сферической поверхности ударника
При прохождении ударником преграды, первый теряет 20-23% скорости. Значительные пластические деформации ударника можно наблюдать при скорости встречи 800 м/с. Можно заметить, что с увеличением скорости ударника растет и количество выбиваемых частиц стекла так как волна напряжений в стекле возрастает до 2400 МПа (в области контакта ударника со стеклом), вовлекая в предельные значения все большее количество элементов.
Во время пробития ударником его движением в среде полагается материал самой плиты. Однако это не всегда так. Например, движение ударника может вначале происходить как в воздушной, так и водной средах. В нашем случае среда считается воздушной, поэтому её влияние на процесс проявляется слабо и не учитывается. Соответственно, сила трения сопротивления материала, при высоких скоростях, начинает расти пропорционально квадрату скорости:
![]() (7)
(7)
где ![]() - коэффициент трения материалов.
- коэффициент трения материалов.
В связи с этим растет и температура трущихся поверхностей ударника и материалов плиты.





