ГУБКА МЕНГЕРА КАК ИНСТРУМЕНТ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПОРИСТОЙ СТРУКТУРЫ АКТИВИРОВАННЫХ УГЛЕЙ
Конференция: CCLXII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Химия

CCLXII Студенческая международная научно-практическая конференция «Молодежный научный форум»
ГУБКА МЕНГЕРА КАК ИНСТРУМЕНТ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПОРИСТОЙ СТРУКТУРЫ АКТИВИРОВАННЫХ УГЛЕЙ
THE MENGER SPONGE AS A MATHEMATICAL TOOL FOR MODELLING ACTIVATED CARBONS POROUS STRUCTURE
Irina Grigorieva
Grade student of MBOU lyceum No.3, Russia, Irkutsk
Michael Perfileev
Scientific adviser, PhD in mathematics, Doctor of International Academy of Natural History, Russia, Irkutsk
Аннотация. Данная работа относится к области математической химии и посвящена геометрическому моделированию пористой структуры активированных углей при помощи губки Менгера. Губка менгера является трехмерным аналогом ковра Серпинского и относится к классу конструктивных фракталов. Идея работы заключается в аналогии между структурой губки Менгера и пористой структурой активированного угля, содержащей поры с различными эффективными радиусами. На основе этой аналогии получена формула для количества итераций губки, приближающих ее структуру к структуре данной марки активного угля.
Abstract. This work pertains to the field of mathematical chemistry and is devoted to geometric modeling of the porous structure of activated carbons using a Menger sponge. The Menger sponge is a three-dimensional analogue of the Sierpinski carpet and belongs to the class of constructive fractals. The idea of the work lies in the analogy between the structure of the Menger sponge and the porous structure of activated carbon containing pores with different effective radii. Based on this analogy, a formula is obtained for the number of sponge iterations that bring its structure closer to the structure of a given brand of activated carbon.
Ключевые слова: фрактал, размерность Хаусдорфа, конструктивный фрактал, активированный уголь, губка Менгера.
Keywords: fractal, Hausdorff dimension, geometric fractal, activated carbon, Menger sponge.
Введение
Фракталами называют множества, обладающее свойством самоподобия или приближенного самоподобия [1]. То есть структура фрактала является похожей на всех мастштабах ввиду того, что фрактал имеет бесконечное число звеньев. Геометрический смысл фрактала — множество точек в евклидовом пространстве, имеющие дробную метрическую размерность (Минковского, Хаусдорфа) или метрическую размерность, отличающуюся от топологической [2]. Геометрические фигуры, обладающие свойствами самоподобия, но повторяющиеся конечное число раз, называют предфракталами. Особым видом фракталов являются конструктивные фракталы. Такие фракталы строятся поэтапно: изображается основа, затем части основы заменяются на фрагмент, взятый в уменьшенном масштабе, при этом число таких этапов бесконечно [3]. Теория фракталов используется при решении задач в различных областях математики, физики, инженерии, химии, биологии, информатики [4]. Существуют различные методы расчета фрактальной размерности, наиболее строгое понятие — размерность Хаусдорфа [5].
Активированным углем называют пористый материал, который производят из кокса, древесного угля, скорлупы кокосовых орехов и другого сырья. Уникальным свойством активированного угля является огромная площадь его поверхности при малом объеме и малой массе — до 2200 ![]() на 1 грамм.
на 1 грамм.
Активированный уголь применяют в медицине (адсорбция токсинов), в противогазах (адсорбция боевых отравляющих веществ), устройствах для очистки питьевой воды, в пищевой промышленности, в производстве удобрений, в качестве катализатора и электродов литиевых аккумуляторов. Является реакционноспособным соединением (способен к окислению в газовой и жидкой фазах), что объясняется наличием активной двойной связи на его поверхности. Двумя важнейшими механизмами действия активированнного угля являются адсорбция и каталитическое окисление.
Процесс произодства активированного угля заключается в обугливании и активации сырья. Термохимическим способом (сырье пропитывают раствором карбоната калия или хлорида цинка и нагревают, ограничив доступ воздуха) или обработав сырье перегретым водяным паром (или горячим углекислым газом) вскрывают поры, до этого находившиеся в закрытом состоянии. То есть из пор удаляются заполняющие их смолы [6].
Моделирование пористой структуры активированного угля при помощи губки Менгера
Активированный уголь нужно изготавливать с разными размерами пор в зависимости от того, какие по размеру молекулы необходимо удержать на его поверхности.
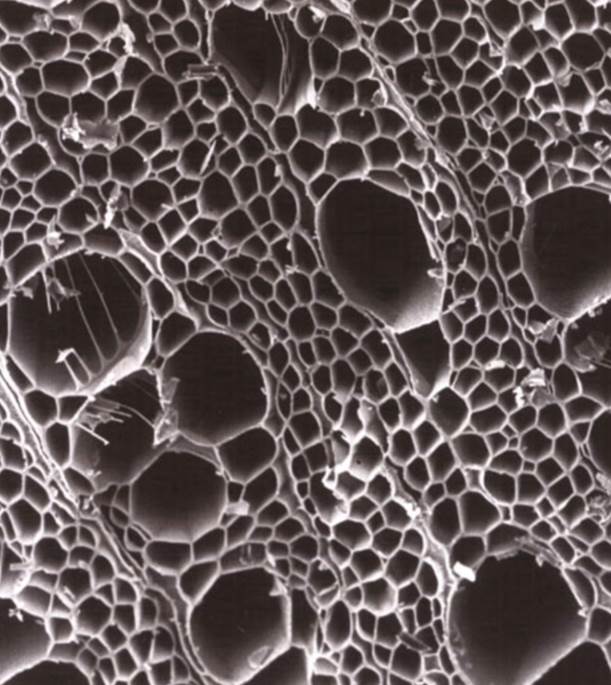
Рисунок 1. Пористая структура древесного активированного угля
Поры активных углей можно классифицировать как супермикропоры (эффективный радиус 0,6-0,7 нм), микропоры (![]() ), мезопоры (
), мезопоры (![]() ), макропоры (эффективный радиус превышает 100-200 нм). За эффективный радиус поры принимают отношение удвоенной площади ее нормального сечения к ее периметру:
), макропоры (эффективный радиус превышает 100-200 нм). За эффективный радиус поры принимают отношение удвоенной площади ее нормального сечения к ее периметру: ![]() . Поры с эффектиным радиусом менее 0,5 нм недоступны для органических молекул; адсорбционная способность зависит от пор с эффективным радиусом 0,5-1,6 нм (сумарный удельный объем таких пор 0,15-0,5
. Поры с эффектиным радиусом менее 0,5 нм недоступны для органических молекул; адсорбционная способность зависит от пор с эффективным радиусом 0,5-1,6 нм (сумарный удельный объем таких пор 0,15-0,5 ![]() ) [7]. В целом замечено, что в активных углях на основе каменного угля велика доля мезопор, у древесных углей преобладает доля макропор, а у «кокосовых» углей больше микропор.
) [7]. В целом замечено, что в активных углях на основе каменного угля велика доля мезопор, у древесных углей преобладает доля макропор, а у «кокосовых» углей больше микропор.
Одним из интереснейших фракталов в трехмерном пространстве является губка Менгера. Для ее построения начальный куб нужно разбить на 27 одинаковых кубиков, а затем извлечь 7 из них: один из центра куба и 6 кубиков из центров граней. Со всеми оставшимися кубиками проводится та же процедура и так далее до бесконечности. Такой процесс вырезания оставляет на каждом шаге 20 кубиков с коэффициентом подобия k=3, поэтому хаусдорфова размерность губки Менгера ![]() [8].
[8].

Рисунок 2. Губка Менгера после трех итераций
Губка Менгера имеет нулевой объем, бесконечную суммарную площадь граней, равную 1 топологическую размерность, а ее ортогональные проекции являются коврами Серпинского. Количество заполненных ящиков равно ![]() , а объем губки после n итераций равен
, а объем губки после n итераций равен
![]() (1)
(1)
[9].
Пусть ![]() - объем твердого вещества в крупинке активированного угля;
- объем твердого вещества в крупинке активированного угля; ![]() - полный объем крупинки, то есть сумма объемов твердого вещества и пор:
- полный объем крупинки, то есть сумма объемов твердого вещества и пор:
![]() . (2)
. (2)
Проведя аналогию между пористой структурой активных углей и губкой Менгера, запишем
![]() . (3)
. (3)
Тогда по определению логарифма и с использованием формулы перехода к новому основанию количество последовательных итераций (процедур вырезания) равно
 . (4)
. (4)
Запишем полный объем крупинки как
![]() (5)
(5)
(т. е. как отношение массы крупинки к плотности данной марки угля), а объем твердого вещества как
![]() . (6)
. (6)
Тогда формула (4) примет вид
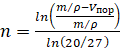 . (7)
. (7)
Полученное в результате расчетов значение n необходимо округлить до целого числа.
Например, 1 грамм активированного угля имеет суммарный объем пор всех размеров 1,4 ![]() , а плотность угля 0,48
, а плотность угля 0,48![]() , т. е. его полный объем составляет 2,08
, т. е. его полный объем составляет 2,08![]() . Если моделировать структуру такого угля при помощи губки Менгера, количество итераций будет равно
. Если моделировать структуру такого угля при помощи губки Менгера, количество итераций будет равно
![]() .
.
Заключение
Таким образом, в данной работе проведено моделирование пористой структуры активированных углей при помощи особого геометрического фрактала - губки Менгера (этот фрактал относится к классу конструктивных фракталов, поэтому представляет наибольший интерес для поставленных в работе целей). Произведен вывод формулы для количества итераций губки, сопоставляющих ее структуру с пористой структурой активированного угля. Также в работе приведен пример расчетов для конкретного случая параметров активного угля.





