ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ЛИНЕЙНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ СЧЁТНЫХ СИСТЕМ ОДУ
Конференция: CL Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

CL Студенческая международная научно-практическая конференция «Молодежный научный форум»
ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ЛИНЕЙНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ СЧЁТНЫХ СИСТЕМ ОДУ
UNIQUENESS OF THE SOLUTION OF A LINEAR BOUNDARY VALUE PROBLEM FOR COUNTING SYSTEMS OF ODE
Madina Gazdieva
Student Ingush State University, Russia, Magas
Ismail Tankiev
Scientific adviser, Candidate of physical and mathematical sciences, Head of the Department of Mathematical Analysis, Professor, Ingush State University, Russia, Magas
Аннотация. В данной статье рассматривается линейная краевая задача для счётных систем обыкновенных дифференциальных уравнений, а также доказывается единственность её решения.
Abstract. This article considers a linear boundary value problem for countable systems of ordinary differential equations, and also proves the uniqueness of its solution.
Ключевые слова: линейная краевая задача, интегральные уравнения, счётные системы ОДУ, единственность решения.
Keywords: linear boundary value problem, integral equations, counting systems of ODE, uniqueness of a solution.
Рассматривается счетная система обыкновенных дифференциальных уравнений
![]()
с краевыми условиями

где ![]() ( j = 1, 2, …), а
( j = 1, 2, …), а ![]() - некоторые действительные числа, такие что
- некоторые действительные числа, такие что

Главный определитель этой системы

а ![]() алгебраические дополнения s – го элемента j - го столбца
алгебраические дополнения s – го элемента j - го столбца![]()
Причем

Теорема : Пусть для задачи (1), (2) выполнены условия (3), (4), (5) и кроме того


где

Тогда в области G, где
![]()

задача (1), (2) имеет по крайней мере одно непрерывное решение
![]()
Если же при этом

то решение будет единственным.
Доказательство: Пусть существуют два решения ![]() и
и ![]() для
для


Оценивая их разность, получим:



Отсюда

Суммируя левые и правые части по i, имеем:
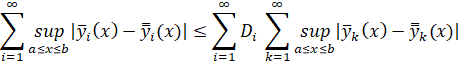
или

что противоречит условию 2) теоремы. Поэтому ![]() Но (4) эквивалентно задаче (1), (2), то существование и единственность решения исходной задачи доказано [1-3].
Но (4) эквивалентно задаче (1), (2), то существование и единственность решения исходной задачи доказано [1-3].





