МОДЕЛИРОВАНИЕ ОБРАЗОВАНИЯ НЕДИССИПАТИВНЫХ СТРУКТУР В СМЕКТИЧЕСКИХ ЖИДКИХ КРИСТАЛЛАХ В НАКЛОННЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ
Секция: 3. Физические науки
лауреатов
участников
лауреатов


участников



XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: естественные и медицинские науки»
МОДЕЛИРОВАНИЕ ОБРАЗОВАНИЯ НЕДИССИПАТИВНЫХ СТРУКТУР В СМЕКТИЧЕСКИХ ЖИДКИХ КРИСТАЛЛАХ В НАКЛОННЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ
Жидкие кристаллы это функциональный наноструктурированный материал, который широко используется в различных системах отображения информации и представляющий интерес, как в плане фундаментальных исследований, так и в плане возможности широкого приложения результатов таких изысканий в технике, материаловедении, дефектоскопии и т.д. Технические потребности в оптических компонентах на основе жидких кристаллов (ЖК), а так же, новые знания, полученные в теории жидких кристаллов, не только стимулируют исследование проблем, связанных с практическими приложениями, но часто заставляют переосмыслить общее отношение к соответствующему разделу науки [6, с.96].
Жидкокристаллическое состояние характеризуется упорядоченным расположением молекул жидкости, у которых оси параллельны [1, с.51]. Ориентационный порядок в расположении молекул создаёт анизотропию: показатель преломления света, диэлектрическая проницаемость, удельное электрическое сопротивление, вязкость и многие другие различные свойства, которые зависят от направления. Структура жидких кристаллов легко изменяется под действием давления, электрического поля и нагрева. Это явление даёт возможность управлять их свойствами путём слабых воздействий и делает жидкие кристаллы незаменимыми материалами для изготовления очень чувствительных индикаторов [6, с.64].
Ориентацией молекул ЖК можно управлять довольно слабыми магнитными, электрическими и температурными полями, что широко используется в приборостроении. Ряд результатов в исследовании нематических жидких кристаллов во внешних магнитных и электрических полях в части влияния особых граничных условий на распределение поля директора в объеме ЖК приведены в [4, с.93]. Влияние периодических граничных условий на распределение поля директора в объеме образца нематика изложено в [3, с.42]. Процесс получения периодических макроструктур в образце НЖК во внешних электрических полях описан в [2, с.29].
На основе жидких кристаллов изготавливают медицинские термометры, датчики температуры для контроля перегрева узлов и деталей, преобразователи невидимого инфракрасного излучения в видимый свет. В последнем случае поглощение инфракрасного излучения нагревает жидкий кристалл так, что изменяется окраска отраженного света. Жидкие кристаллы применяют в модуляторах, системах отображения информации – калькуляторах, часах, измерительных приборах, устройствах для отклонения светового потока и др.
Рассмотрим тонкий слой смектического жидкого кристалла SmC* во внешнем электрическом поле, прикладываемом под углом ![]() к слою смектика.
к слою смектика.

Рисунок 1. Геометрия смектического ЖК во внешнем электрическом поле (a) – страйп-структуры на подложках; (b) ![]() – азимутальный угол; (c)
– азимутальный угол; (c) ![]() – угол приложения электрического поля к образцу
– угол приложения электрического поля к образцу
В рассматриваемом образце ЖК SmC* в геометрии «bookshelf» (Рис. 1) электрическое поле ![]() приложено под углом
приложено под углом ![]() к нормали к плоскости смектических слоев. Вектор
к нормали к плоскости смектических слоев. Вектор ![]() , представляющий единичный вектор проекции директора n описывается азимутальным углом
, представляющий единичный вектор проекции директора n описывается азимутальным углом ![]() , показанным на рис. 2(b).
, показанным на рис. 2(b).
Распределение директора по верхней и нижней границам вдоль оси Oy имеет периодический характер, вдоль оси Oz – направление единичного вектора ![]() .
.
В работе [5, с.129] было предложено динамическое уравнение в одноконстантном приближении, описывающее перераспределение поля директора СЖК во внешнем электрическом поле
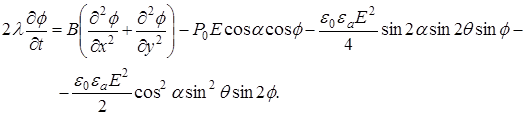 (1)
(1)
Статическое уравнение принимает вид, анализ которого проведен в работе [5, с.129-133]:
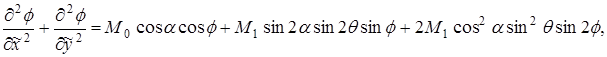 (2)
(2)
где 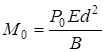 ,
, 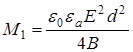 ,
, ![]() ,
, ![]() (для удобства далее знак волны над переменными x и y будем опускать).
(для удобства далее знак волны над переменными x и y будем опускать).

Рисунок 2. Граничные условия, использованные для решения уравнения (1)
Граничные условия
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (3)
. (3)
Численное решение может быть найдено при дискретизации уравнения (2) внутри прямоугольной области (N + 2)´(M + 2)
 ,
, 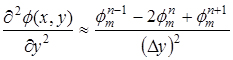 .
.
Разностное уравнение
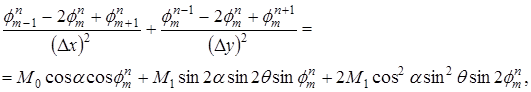
Граничные условия Дирихле примут следующий разностный вид
![]() ,
, ![]() ,
, ![]() ,
, ![]() для
для ![]() ,
, ![]() .
.
Полученная выше система при малых ![]() может быть линеаризована и решена различными простыми методами. При использовании метода мнимых линий мы получаем систему обыкновенных дифференциальных уравнений
может быть линеаризована и решена различными простыми методами. При использовании метода мнимых линий мы получаем систему обыкновенных дифференциальных уравнений
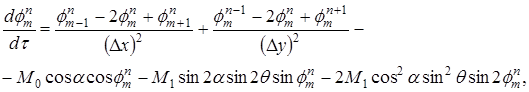
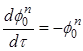 ,
, 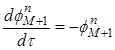 ,
, 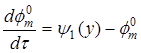 ,
, 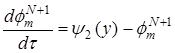 .
.
При этом должно выполняться условие  . Здесь и далее
. Здесь и далее 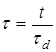 ,
, 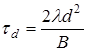 .
.
В данной статье функции ![]() ,
, ![]() задаются следующим образом:
задаются следующим образом:
![]() ,
, ![]() , (4)
, (4)
![]() ,
, ![]() , (5)
, (5)
где: функция Хевисайда доопределена в точке ноль ![]() .
.
Расчеты проведены для следующих значений физических параметров системы: ![]() Ф/м,
Ф/м, ![]() Н,
Н, ![]() ,
, ![]() Кл/м,
Кл/м, ![]() м,
м, ![]() ,
, ![]() , E=5×102 В/м.
, E=5×102 В/м.
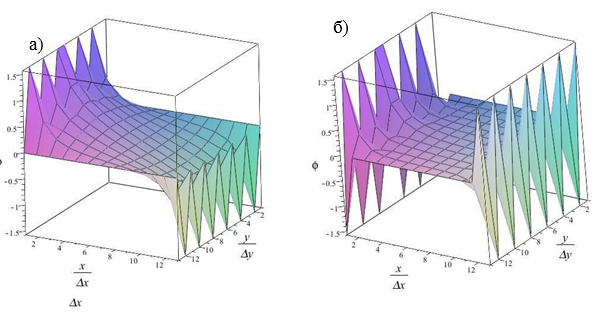
Рисунок 3. Зависимость ![]() , рассчитанная для
, рассчитанная для ![]() ,
, ![]() для случая (4) – б) и (5) – а)
для случая (4) – б) и (5) – а)
Вычисления выполнены в Maple 15 методом линий [7, с.32-35]. Полученные результаты подтверждают возможность управления процессами структурообразования с помощью обработки, ограничивающих образец жидкого кристалла, подложек. При исследовании интерес представляли периодические структуры на границах раздела и их влияние на распределение поля директора в объеме. Наблюдаемый в ходе численного эксперимента эффект переориентации поля директора в объеме образца ЖК под влиянием периодических структур, полученных на подложках, подтверждает достоверность результатов изложенных в [5, с.133]. Метод линий показал в данной работе свою эффективность, но в то же время при увеличении количества узловых точек время счета и требуемые ресурсы при выполнении расчетов на персональных компьютерах довольно велики. Поэтому при достаточно малых периодах, используемых на подложках, возникает необходимость уменьшения длины шага дискретизации по осям. В этом случае вычислительный процесс целесообразно строить с привлечением распараллеливания, что позволит увеличить скорость счета.
Работа выполнена при поддержке Академии наук Республики Башкортостан и Российского Фонда Фундаментальных Исследований в рамках проекта № 14-02-97026.
Список литературы:
1. Блинов Л.М. Жидкие кристаллы: структура и свойства. М. Книжный дом «ЛИБРОКОМ», 2013 – 480 с.
2. Кондратьев Д. В., Мигранов Н. Г. Континуальная подход в теории жидких кристаллов: монография – Уфа: Гилем, Башк. энцикл., 2013. – 164 с.
3. Кондратьев Д. В., Мигранов Н. Г. Построение функционала, описывающего макроструктуры в тонком слое нематического жидкого кристалла // Вестник ЧелГУ. Физика. Вып. 7. 2010. №12. С. 41-46.
4. Кондратьев Д. В., Мигранов Н. Г. Распределение молекул нематического жидкого кристалла в полупространстве, ограниченном структурированной подложкой // Вестн. Помор. ун-та. Сер. Естествен. науки. 2009. № 3. С. 91–95.
5. Кондратьев Д. В., Мигранов Н. Г., Мигранова Д. Н. Исследование устойчивости равновесных состояний наноматериалов на основе сегнетоэлектрических жидких кристаллов во внешнем электрическом поле // Жидк. крист. и их практич. использ. 2015. Т. 15, № 3. С. 133–142.
6. Пикин, С.А. Жидкие кристаллы / С.А. Пикин, Л.М. Блинов / Под ред. Л.Г. Асламазова. – М.: Наука, 1982. – 208 с.
7. Northrop Paul W. C., Ramachandran P. A., Schiesser W. E., Subramanian V. R. A robust false transient method of lines for elliptic partial differential equations. Chemical Engineering Science. 2013. Vol. 90. P. 32–39.

