Использование пакета Maple для решения логических выражений на уроках информатики
Конференция: XLI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: гуманитарные науки»
Секция: Педагогика
лауреатов
участников
лауреатов


участников



XLI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: гуманитарные науки»
Использование пакета Maple для решения логических выражений на уроках информатики
Введение
В последнее время в образовании стали использоваться различные информационные технологии, в том числе компьютерные математические пакеты AutoCad, MatLab, Maple, Mathematica и другие. Применение данных инструментальных средств на уроках информатики разрешает решать сложные задачи, производить большие математические преобразования, не допуская при этом просчётов. При использовании средств, которые не делают ошибок, ученик убеждён, что ошибки не будет и чувствует себя более уверенным. При этом, время решения задачи сокращается. Система компьютерной алгебры (СКА) Maple позволяет сформировать свою библиотеку процедур, при их разработке у ученика формируется умение программирования, а при использовании закрепляются различные математические знания и навыки. Ниже описываются основные особенности Maple, демонстрирующие его возможности для решения конкретных образовательных задач математики, информатики.
Описание пакета Maple
В основе пользовательского интерфейса СКА Maple лежит графический многооконный интерфейс операционной системы Windows, который является простым, интуитивно понятным и интерактивным. Одна из важнейших особенностей СКА Maple – строгое (и очень удачное) соответствие структуры команд и программных процедур логике математического мышления. Команды и процедуры СКА Maple оказывают влияние на переменные и параметры подобно функциям многих переменных, поэтому грамотное владение СКА Maple подразумевает умение работать с математическими функциями. Необходимо отметить, что сама эта особенность существенно повышает математическую грамотность и развивает абстрактное математическое мышление. «СКА Maple обучает правильному пониманию математических выражений – как совокупности символов, присутствие которых обязательно, а порядок применения принципиально важен» [5, с. 460].
В рамках школьного курса на уроках информатики изучается алгебра логики. С помощью СКА Maple возможно решать логические задачи, определять истинность или ложность высказываний. «В среде СКА Maple для логических выражений предусмотрен специальный тип переменных – boolean. Произвольное выражение имеет тип Boolean, которые он имеет тип relation, или тип Logical или является одной из булевых констант: true, false, или FAIL. Таким образом для выполнения логических операций СКА Maple использует трехзначную логику. Специальные имена True и False используются для представления логической истины и ложности. Третье специальное название FAIL (СБОЙ, не определен) используется для представления выражения, истинность которого неизвестна» [4, с. 311].
Тип relation образует арифметические выражения, в которые входят отношение `=`, `<>,` < `, or` <= `. Выражение имеет тип Logical, если в него входят логические операции `and`,` or`, `xor`,` implies` и `not`. Для проверки типа логического выражения используется команда type:
> type (8 <10 and x> 5, boolean);
> type (x <17, relation);
> type (c and not b, logical);
«Для вычисления логических выражений используется команда evalb (B), которая возвращает возможные значения логического выражения B: true, false, and FAIL. Если вычисления невозможны, то возвращается само выражение B» [4, с. 313].
Рассмотрим три базовые логические операции – конъюнкция, дизъюнкция, отрицание.
Таблица 1.
Основные логические операции
|
|
Конъюнкция |
Дизъюнкция |
Инверсия |
|||||
|
Название |
логическое умножение |
логическое сложение |
отрицание |
|||||
|
Обозначение |
А&В или А |
А |
|
|||||
|
Союз в естественном языке |
А и В |
А или В |
Не А |
|||||
|
Таблица истинности |
А |
В |
А&В |
А |
В |
А |
А |
¬А |
|
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Если на уроке необходимо составить таблицу истинности для некоторой функции, то можно воспользоваться возможностями СКА Maple.
«Язык программирования СКА Maple использует трехзначную логику, описанную ранее. Взаимный переход между этими двумя логическими системами реализуется командами Export ( ) и Import ( )» [6, с. 131]. Export переводит логическое выражение двузначной логики пакета Logic в соответствующее ему логическое выражение трехзначной логики СКА Maple. Команда Import имеет аналогичный синтаксис.
В этой программе есть пакет Logic, в котором находятся следующие команды: &and, &iff, &implies, &nand, &nor, ¬, &or, &xor, BooleanSimplify, Canonicalize, Contradiction, Dual, Environment, Equivalent, Export, Implies, Import, Normalize, Random, Satisfy, Тautology, TruthTable.
Пример 1. Составить таблицу истинности для функции А Ú ¬В
Сначала подключаем пакет Logic:
>with(Logic)
[&and, &iff, &implies, &nand, &nor, ¬, &or, &xor, BooleanSimplify, Canonicalize, Contradiction, Dual, Environment, Equivalent, Export, Implies, Import, Normalize, Random, Satisfy, Tautology, TruthTable]
Затем вводим следующие команды:
>Import(A or (not B), form = boolean)
A &or ¬(B)
>TruthTable(A &or (¬ B), [A,B]) (TruthTable создаёт таблицу истинности для заданного логического выражения)
table([(false, false) = true, (false, true) = false, (true, false) = true, (true, true) = true])
В итоге получается по дизъюнкции ложь только тогда, когда оба выражения ложны.
Другой пример. Если необходимо указать, когда выражение истинно, а когда ложно 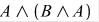 , то сначала подключаем пакет Logic. Затем, вводим команду Import() и строим таблицу истинности TruthTable. В итоге получатся следующие результаты:
, то сначала подключаем пакет Logic. Затем, вводим команду Import() и строим таблицу истинности TruthTable. В итоге получатся следующие результаты:
>with(Logic)
[&and, &iff, &implies, &nand, &nor, ¬, &or, &xor, BooleanSimplify, Canonicalize, Contradiction, Dual, Environment, Equivalent, Export, Implies, Import, Normalize, Random, Satisfy, Tautology, TruthTable]
>Import(A and (A and B), form = boolean)
A &and (A &and B)
>TruthTable(A &and (A &and B), [A, B])
Table ([(false, false) = false, (false, true) = false, (true, false) = false, (true, true) = true])
Вывод
Таким образом, использование Maple позволяет обеспечить организацию самостоятельной работы учащихся и эффективное решение одной из задач контроля и проверки знаний обучаемых по учебному предмету. В статье рассмотрены решения некоторых задач в Maple.

 В
В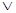 В
В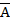
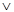 В
В