Корреляционный анализ стоимости удобрений сахарной свёклы на примере предприятий Ливенского и Должанского районов Орловской области

CORRELATION ANALYSIS OF THE COST OF SUGAR BEET FERTILIZERS ON THE EXAMPLE OF ENTERPRISES OF LIVENSKY AND DOLZHANSKY DISTRICTS OF ORYOL REGION

Elena Volynkina

Student, Oryol state University named after N.V. Parakhin, Russia, Orel

Natalya Yakovleva

Candidate of economic Sciences, associate Professor, Oryol state University named after N.V. Parakhi, Russia, Orel

Аннотация. В данной статье мы проводим корреляционный анализ стоимости удобрений сахарной свёклы с целью рассмотреть силу влияния урожайности на уровень стоимости удобрений сахарной свёклы.

Abstract. In this article, we conduct a correlation analysis of the cost of sugar beet fertilizers in order to consider the impact of yield on the level of cost of sugar beet fertilizers.

Ключевые слова: корреляционный анализ, стоимость удобрений, сахарная свёкла, урожайность, регрессии, коэффициент эластичности, дисперсия, результативный и факторный признаки.

Keywords: correlation analysis, cost of fertilizers, sugar beet, yield, regression, coefficient of elasticity, dispersion, effective and factor characteristics.

С помощью корреляционного анализа представляют взаимосвязи между признаками в виде математического уравнения, на основе которого исчисляют показатели, дающие количественную характеристику связи, а также дают статистическую оценку достоверности характеристик связи.

Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функций и между аргументом и функцией нельзя установить строгой зависимости, называется корреляционной [2, с. 24]. Корреляционную связь можно установить при изучении массовой статистической совокупности в виде общей тенденции.

Уравнение парной линейной корреляционной связи называется уравнением регрессии и имеет вид:

,                                                                                                            (1)

где  – теоретическое значение результативного признака;

х – факторный признак;

а – параметр уравнения, который не имеет экономического смысла;

b – коэффициент регрессии [3, 56].

Проведём корреляционный анализ на примере зависимости между стоимостью затрат на удобрения в расчёте на 1 га посева сахарной свёклы Ливенского и Должаского районов Орловской области (результативный признак) и её урожайностью (факторный признак). С целью проведения корреляционного анализа построим таблицу.

Таблица

Исходные данные по группе предприятий Должанского и Ливенского районов Орловской области для проведения корреляционно-регрессионного анализа, отражающего связь между затратами на удобрения и урожайностью сахарной свёклы 2018 г

Воспользуемся формулами для вычисления параметров уравнения регрессии:

                                                                                                                (2)

                                                                                                                 (3)

Подставив значения, получаем:

Линейное уравнение примет вид:

=396,1+2,5 * х

Полученное уравнение показывает, что с увеличением затрат на 1 га посева, урожайность сахарной свёклы возрастает в среднем на 2,5 ц с 1 га убранной площади.

Подставляя в полученное уравнение х_i из исходных данных, определим теоретические (выровненные) значения результативного признака. Занесём полученные значения в таблицу.

При линейной корреляции между Х и Y исчисляют парный линейный коэффициент корреляции r. Оценим тесноту связи между изучаемыми признаками с помощью коэффициента корреляции, который определяется по формуле:

                                                                                           (4)

где: ,  - среднее квадратическое отклонение в ряду х и в ряду у.

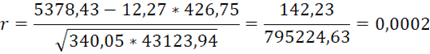
Связь между факторами прямая и в соответствии со шкалой Чеддока характеризуется как слабая.

Для оценки силы связи признаков Х и Y также найдём средний коэффициент эластичности, который показывает, на сколько процентов в среднем по совокупности изменится значение результативного признака от своей средней величины при изменении факторного признака на 1 % от своего среднего значения (формула 5):

 ,                                                                                                               (5)

Подставим значения и получим:

Таким образом, в среднем на 0,02 % по совокупности изменится урожайность сахарной свёклы от своей средней величины при изменении затрат на 1 га посева на 426,78.

Чтобы проверить, насколько полученные результаты правильно реальные данные необходимо качество полученного уравнения оценить с помощью F-критерия Фишера по формуле 6:

 ,                                                                                                       (6)

Установим табличное значение F-критерия Фишера (а=0,05).

При уровне значимости 0,05, F_табл. = 5,99. Следовательно, при заданном уровне, мы отвергает нулевую гипотезу о статистической незначимости.

Так как уравнение регрессии является статистически незначимым, расчёт прогнозируемого значения себестоимости 1 ц сахарной свёклы по данному уравнению не даст достоверного результата.