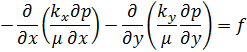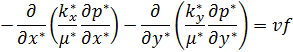Моделирование фильтрации жидкости в неоднородных ортотропных пористых средах
Журнал: Научный журнал «Студенческий форум» выпуск №38(89)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №38(89)
Моделирование фильтрации жидкости в неоднородных ортотропных пористых средах
Исследовательская работа предназначена для моделирования процесса движения однофазной жидкости в неоднородной ортотропной пористой среде[1-3]. Актуальность исследования связана, в первую очередь, с возможностью прогнозирования процессов, протекающих в нефтяных пластах при разработке месторождений. Однако, многие работы включают простые предположения, что среда является однородной и изотропной. Игнорирование особенностей этой среды может оказать существенное влияние на результаты моделирования, что в свою очередь может снизить показатели подачи нефти. В этой работе проводится моделирование процесса фильтрации с коэффициентом проводимости в виде диагонального тензора, а пористость – в виде функции давления, близкого к значениям конкретных месторождений. Это существенно затрудняет постановку задачи, а также ее количественное решение. Цель работы-разработка алгоритмов для цифровой реализации модели движения однофазной жидкости в неоднородной ортотропной пористой среде.
Актуальность рассматриваемого отчета в работе, в первую очередь, связана с использованием в теории разработки месторождений аномальной нефти. Такие расчеты используются для обработки коллекторов низкой и более низкой проводимости, разработки газовых месторождений, изучения движения не ньютонных, вязких пластиковых жидкостей. В этой работе были изучены качественные свойства четырех количественных методов реализации модели, характеризующих движение жидкости в анизотропной среде, количественно обоснованы устойчивость и комплектность разностных схем. Получение графиков, отражающих данный физический процесс.
Постановка задачи.
Рассмотрим движение жидкости L в однородной пористой среде без учета однофазных и гравитационных сил в прямоугольной двухмерной области.Этот физический процесс характеризуется следующими уравнениями:
1. уравнение непрерывности:
|
|
(1)
|
где:
![]() - пористость;
- пористость;
![]() - плотность жидкости;
- плотность жидкости;
![]() - скорость движения жидкости;
- скорость движения жидкости;
![]() ,
,![]() - компоненты вектора скорости;
- компоненты вектора скорости;
q- источник движения (например, скважина);
2. уравнение движения, характеризующееся линейным законом Дарси:
|
|
(2) |
|
|
(3) |
где:
![]() - давление жидкости;
- давление жидкости;
![]() - вязкость;
- вязкость;
K- абсолютная проводимость среды;
В изотропной среде величину K можно принимать стабильно, а в анизотропной среде K-симметричный линейный ортогональный тензор второго ранга:
|
|
(4) |
![]()
![]()
3. уравнение состояния жидкости:
|
|
(5) |
где:
![]() – коэффициент сжимаемости жидкости;
– коэффициент сжимаемости жидкости;
![]() и
и ![]() – начальное давление и плотность жидкости;
– начальное давление и плотность жидкости;
Основным признаком этого расчета является давление жидкости. Остальные знаковые узорятся под давлением.
Давайте сделаем дополнительные суждения о физическом процессе. Например, L-пусть будет несжимаемой и однородной жидкостью, то есть ρ=const. В этом случае, можно убедиться в том, что при непосредственных вычислениях![]() . Давайте сделаем дополнительные суждения о физическом процессе.
. Давайте сделаем дополнительные суждения о физическом процессе.
С учетом вышеуказанных соображений уравнение непрерывности (8) имеет следующий вид:
|
|
(6) |
Теперь рассмотрим расчет уравнений(8)-(12) в удобном виде. Для этого уравнения (9) и (10) (8) переносят уравнения непрерывности (8):
|
|
(7) |
Присвоить граничных условиях второго рода на границе области:
![]()
(7) в результате преобразования уравнения к непереносному виду приводится к следующему виду.
|
|
(8) |
Для реализации приведенного выше уравнения (8) используем итерационные алгоритмы.
В ходе расчетной практики можно увидеть следующие результаты:
|
|
|
|
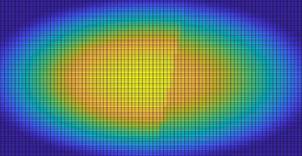
Рисунок 1. Результаты метода Зейделя при наличии h=1/100 |
Рисунок 2. Результаты метода Зейделя при наличии h=1/50 |
|
|
|
|
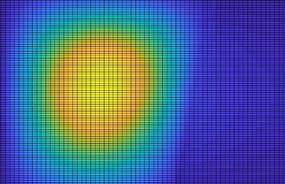
Рисунок 3. Результаты метода переменных направлений при h=1/100 |
Рисунок 4. Результаты метода переменных направлений при h=1/50 |