Исследование влияния методов локальной оптимизации на классифицирующие способности многослойного и нечеткого многослойного персептронов при решении задачи классификации

Введение. В настоящее время одной из наиболее популярных задач, решаемых с помощью нейронных сетей, остается задача классификации: распознавание рукописных цифр, классификация клиентов по степени рисков, распознавание лиц с камеры. Еще одним примером задачи классификации является распознавание типа дорожного покрытия при движении автомобиля: щебеночные покрытия, гравийные, грунтовые поверхности, сборные цементные конструкции, асфальтовые или мощеные покрытия. В настоящее время данная задача приобретает все большую актуальность в связи с ростом популярности проектирования и конструирования автопилотируемых транспортных средств. Распознавание типа дорожного покрытия позволит автомобилю принять решение о том, какой скоростной режим допустим в данной ситуации.

Задача классификации – задача, в которой имеется множество объектов, разделенных некоторым образом на классы. Требуется построить алгоритм, способный классифицировать произвольный объект (указать номер класса, к которому относится данный объект) из исходного множества [1].

Нейронные сети оказались очень полезными при решении задач распознавания образов и классификации объектов. Они способны решать задачи, в которых неизвестны зависимости между входными и выходными данными [2]. Известны и другие, более традиционные подходы для решения задачи классификации (например, наивный байесовский классификатор или линейный дискриминант Фишера), однако они не обладают необходимой гибкостью за пределами ограниченных условий.

В данной работе для решения задачи классификации используются многослойный и гибридный нечеткий многослойный персептроны. Исследованы классифицирующие способности этих нейронных сетей различной конфигурации.

Основная часть. Наиболее популярный класс многослойных сетей прямого распространения образуют многослойные персептроны, в которых каждый вычислительный элемент использует в качестве функции активации сигмоидальную функцию или гиперболический тангенс. При этом многослойный персептрон в целом может формировать сколь угодно сложные границы принятия решения, несмотря на то что элементы по отдельности имеют очень ограниченные вычислительные возможности [3]. Разработка алгоритма обратного распространения ошибки для определения весов в многослойном персептроне сделала эти сети наиболее популярными у исследователей и пользователей нейронных сетей.

Гибридный нечеткий многослойный персептрон является модификацией классического многослойного персептрона с дополнительным слоем с нечеткой самоорганизацией. Благодаря наличию нечеткого слоя нечеткий многослойный персептрон способен определять степень принадлежности входного вектора к одному из возможных классов, что позволяет решать задачи с пересекающимися классами. Структура нечеткого многослойного персептрона представлена на рисунке 1.

Обучение многослойного персептрона заключается в минимизации целевой функции и включает в себя определение направления оптимизации, выбор величины шага в направлении оптимизации и определение нового решения.

Существует несколько способов подбора коэффициента обучения (шага в направлении оптимизации), в данной работе была выбрана формула корректировки значения в зависимости от итерации обучения:

                                                                                                               (1)

где  – начальное значение коэффициента обучения,  – константа времени поиска, задаваемая пользователем, а t – номер итерации обучения.

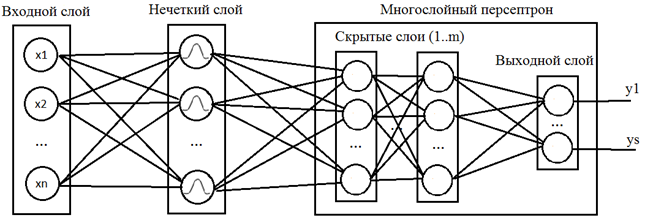
Рисунок 1. Структура нечеткого многослойного персептрона

Для повышения эффективности метода наискорейшего спуска был выбран метод обучения с моментом, при котором пересчет весов сети производится по формуле:

,                                                                    (2)

где первое слагаемое соответствует алгоритму наискорейшего спуска, а второе учитывает последнее изменение весов и не зависит от фактического значения градиента.

Результаты.

В качестве выборки для обучения и тестирования нейронной сети были выбраны данные с датчиков, фиксировавших положение некоторой детали автомобиля в пространстве при прохождении различных дорожных покрытий. В данной выборке представлено 6 классов дорожных покрытий (следовательно, требуется 6 выходных значений нейронной сети), 5 входных параметров, включая номер типа детали, номер детали и координаты положения данной детали (x, y, z). Всего в выборке представлено 18000 записей.

Обучение нейронной сети осуществлено с помощью метода обратного распространения ошибки. Обучение нечеткого слоя нечеткого многослойного персептрона произведено с помощью алгоритма нечеткой самоорганизации C-means. Размеры входного и выходного слоев для всех экспериментов установлены в соответствии с количеством атрибутов и классов. Наборы разбиты на обучающую и тестовую выборки в соотношении 7 к 3. В качестве методов локальной оптимизации используются метод подбора коэффициента обучения и метод наискорейшего спуска с моментом.

Исследование зависимости погрешности обучения от фиксированного значения коэффициента обучения представлено на рисунке 2.

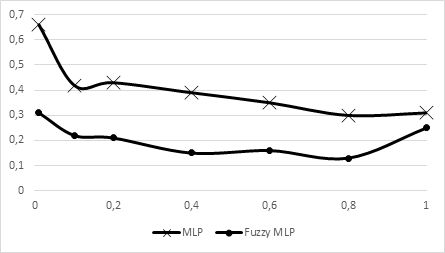
Рисунок 2. График зависимости погрешности обучения от фиксированного значения коэффициента обучения

Исследование зависимости погрешности обучения от начального значения коэффициента обучения представлено на рисунке 3.

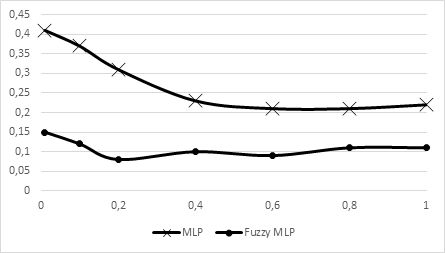
Рисунок 3. График зависимости погрешности обучения от начального значения коэффициента обучения

Исследование зависимости погрешности классификации от значения момента представлено на рисунке 4.

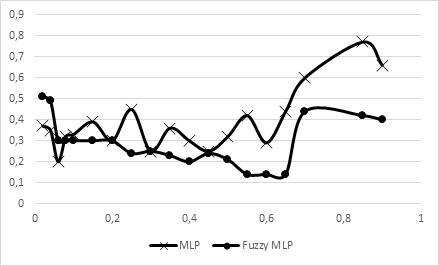
Рисунок 4. График зависимости погрешности классификации от значения момента

Выводы. Таким образом, из графиков видно, что обучаемость и классифицирующие способности нейронных сетей проявляются лучше при использовании методов локальной оптимизации. При достаточно больших начальных значениях коэффициента обучения и при большом числе итераций веса лучше сходятся к своим оптимальным значениям. При больших значениях момента происходит резкое ухудшение классифицирующих возможностей. При этом нечеткий многослойный персептрон показал более точные результаты в сравнении с многослойным персептроном. Однако, обучение нечеткого многослойного персептрона требует большего числа итераций и больших затрат памяти вычислительной машины.