Алгоритм FAST-SLAM: фильтр Калмана
Журнал: Научный журнал «Студенческий форум» выпуск №17(68)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №17(68)
Алгоритм FAST-SLAM: фильтр Калмана
Метод одновременной навигации и картографирования (SLAM – Simultaneous Localization and Mapping) является одним из наиболее актуальных подобластей робототехники. Понятие процесса SLAM на интуитивном уровне можно представить на простом примере.
Представим простой мобильный робот, оснащенный набором колес, соединенных с двигателем, и камерой.
Такой небольшой набор представляет собой физическое устройство, способное изменять скорость и направление движения. Допустим, что наш робот управляется удаленно.
Приводы позволяют роботу перемещаться, а камера обеспечивает достаточную визуальную информацию для оператора, чтобы понять, где находятся окружающие объекты и как робот ориентирован по отношению к ним. То, что делает человек – оператор – это пример SLAM.
Существует множество алгоритмов реализации метода SLAM, отличающихся друг от друга использованием разных аппаратных средств и алгоритмов вычислений.
Общая постановки задачи всех методов SLAM следующая: вычисление оценок локализации робота и ориентиров на строящейся карте путем обработки данных, считываемых с датчиков.
Наиболее распространенными из них являются Vision SLAM (V-SLAM), Distributed Particle SLAM (DP-SLAM), Extended Kalman Filter SLAM (EKF-SLAM) и Fast-SLAM.
Алгоритм Fast -SLAM отличается от остальных вышеуказанных алгоритмов, так как является гибридным методом, в котором сочетаются методы DP-SLAM на основе фильтра частиц и метод EKF-SLAM, основанный на применении фильтра Калмана.
В данной работе будет рассмотрен фильтр Калмана в алгоритме Fast -SLAM.
Алгоритмы SLAM состоят из двух этапов: локализации и картографирования.
Локализация – это процесс определения местоположения робота относительно объектов окружающей среды, которые называются ориентирами. Ориентиры – изначально выделенные объекты окружающей среды, информация о координатах которых используется при локализации мобильного робота. Картографирование – это процесс построения карты окружающей среды, на которой обозначаются координаты ориентиров и мобильного робота.
В алгоритме Fast – SLAM фильтр Калмана используется для предсказывания текущей позиции мобильного робота.
Фильтр Калмана был разработан Р. Е. Калманом. Его работа была опубликована в 1960 году. Фильтр Калмана – это алгоритм, который обрабатывает данные и оценивает переменную. В SLAM переменными, которые необходимо оценивать, являются состояния позиции мобильного робота и местоположения объектов окружающего мира.
Фильтр Калмана представляет собой набор математических уравнений, обеспечивающих эффективное оценивание состояния системы таким образом, чтобы минимизировалась средняя квадратичная ошибка оценки состояния. При этом фильтр Калмана способен поддерживать оценки прошлых, настоящих и будущих состояний. Обобщенный алгоритм фильтра Калмана представлен на рисунке 1.
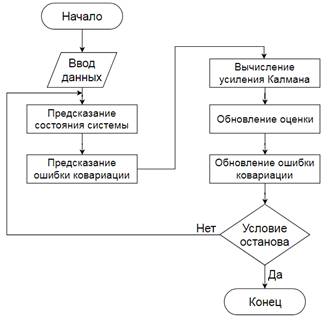
Рисунок 1. Алгоритм фильтра Калмана
Фильтр Калмана решает общую проблему оценивания состояния ![]() , которое можно описать с помощью линейного уравнения:
, которое можно описать с помощью линейного уравнения:
![]() , (1)
, (1)
с измерением ![]() :
:
![]() . (2)
. (2)
Случайные переменные ![]() и
и ![]() представляют некоторый шум.
представляют некоторый шум.
Матриц![]() в уравнении (1) связывает состояние системы на предыдущем шаге
в уравнении (1) связывает состояние системы на предыдущем шаге ![]() с состоянием на текущем шаге
с состоянием на текущем шаге ![]() при отсутствии каких-либо шумов. Матрица
при отсутствии каких-либо шумов. Матрица ![]() связывает управляющее воздействие
связывает управляющее воздействие ![]() с состоянием
с состоянием ![]() . Матрица
. Матрица ![]() в уравнении (2) связывает состояние измерения
в уравнении (2) связывает состояние измерения ![]() .
.
Определим ![]() , чтобы она была априорной оценкой состояния на заданном шаге
, чтобы она была априорной оценкой состояния на заданном шаге ![]() и
и ![]() для апостериорной оценки системы на шаге
для апостериорной оценки системы на шаге ![]() при заданном измерении
при заданном измерении ![]() . Свяжем ошибки определения априорной и апостериорной оценок через уравнения:
. Свяжем ошибки определения априорной и апостериорной оценок через уравнения:
![]() ,
, ![]() .
.
Априорная и апостериорная оценки ошибки ковариации, соответственно, (уравнения 3 и 4):
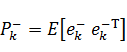 ,
, 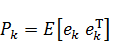 .
.
При выводе уравнения для фильтра Калмана начнем с уравнения, вычисляющего оценку апостериорного состояния системы ![]() , как линейную комбинацию априорных оценок
, как линейную комбинацию априорных оценок ![]() и вычислим разницу между фактическим измерением
и вычислим разницу между фактическим измерением ![]() и предсказанием измерения
и предсказанием измерения ![]() :
:
![]() (5)
(5)
Разность ![]() в (5) называется инновацией измерения или остаточным. Остаточное отражает несоответствие между прогнозируемым измерением
в (5) называется инновацией измерения или остаточным. Остаточное отражает несоответствие между прогнозируемым измерением ![]() и фактическим измерением
и фактическим измерением ![]() . Остаточный ноль означает, что они совпадают друг с другом.
. Остаточный ноль означает, что они совпадают друг с другом.
Матрица ![]() называется коэффициентом усиления или смешивания, которая предназначена для минимизации апостериорной ошибки ковариации (4). Процесс получения данного коэффициента представлен в работе [1].
называется коэффициентом усиления или смешивания, которая предназначена для минимизации апостериорной ошибки ковариации (4). Процесс получения данного коэффициента представлен в работе [1].
Исходя из результатов в работе [1] можно сказать следующее: если ковариация ошибок измерения приближается к нулю, фактическим ![]() измерениям доверяют больше, а предсказанным
измерениям доверяют больше, а предсказанным ![]() – меньше. Если априорная оценка ошибки ковариации приближается к нулю, то фактическим измерениям доверят меньше, а предсказанным – больше.
– меньше. Если априорная оценка ошибки ковариации приближается к нулю, то фактическим измерениям доверят меньше, а предсказанным – больше.
Фильтр Калмана оценивает состояние системы, используя форму управления с обратной связью: фильтр оценивает систему, а потом получает обратную связь в виде измерений с некоторым шумом и выполняет корректировку предсказания. Исходя из этого, уравнения для фильтра Калмана делятся на две группы: уравнения обновления времени (the time update equations) и уравнения обновления измерений (the measurement update equations). Уравнения обновления времени отвечают за предсказывание следующего состояния на основе текущего и оценку ковариации ошибок для получения априорных оценок следующего шага времени. Уравнения обновления измерений предназначены для обратной связи, то есть за включение нового измерения в априорную оценку для получения улучшенной апостериорной оценки.
Уравнения обновления времени дискретного фильтра Калмана:
![]() , (6)
, (6)
![]() . (7)
. (7)
Уравнения обновления измерений дискретного фильтра Калмана:
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() , (10)
, (10)
Первым шагом обновления измерений является вычисление коэффициента усиления Калмана K. Следующий шаг – получение измерения ![]() , а затем вычисление оценки апостериорного состояния путем включения измерений как в (9). Последним шагом является получение ковариационной оценки апостериорной ошибки по (10).
, а затем вычисление оценки апостериорного состояния путем включения измерений как в (9). Последним шагом является получение ковариационной оценки апостериорной ошибки по (10).
После каждого обновления измерения процесс повторятся с предыдущей апостериорной оценкой, которая используется для прогнозирования новых априорных оценок. Этот рекурсивный алгоритм является одним из основных черт фильтра Калмана.
Фильтр Калмана является весьма перспективным методом предсказывания положения ориентиров и позиции робота на основе предыдущего состояния, но в работе фильтра имеется недостаток: накопление ошибки локализации, которая возникает из-за неточности в определении начального положения робота и ориентиров.

