Расчет стоимостных характеристик рекурсивных конвейерных процессов
Журнал: Научный журнал «Студенческий форум» выпуск №15(66)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №15(66)
Расчет стоимостных характеристик рекурсивных конвейерных процессов
При определении цепочки создания стоимости конвейерных процессов необходимо учитывать различные показатели – от затрат материалов на основное производство изделий до расчета затрат на электроэнергию. Подробно эти показатели рассмотрены в таблицах [1, с. 63-86].
Рекурсивный конвейерный процесс, рассматриваемый в статье [2, с. 230-273], описывается орграфом с набором рекурсивных функций. Рекурсивные функции графа цепочки создания стоимости производственного процесса принципиально отличается от функций графа вычисления времен выполнения операций тем, что его основной характеристикой является стоимость выполнения операции.
Формализуем описание графа цепочки создания стоимости.
Рекурсивный конвейерный процесс (РКП) описывается ациклическим орграфом G = (V,A), где V – множество из n вершин, A – множество дуг (пар v,w ![]() V). Вершины графа представляют собой операцию производственного процесса, либо спусковую функцию, определяющую временное предшествование операций. Для определения типа вершины отметим их как отображение type: V→O, где O – множество вида {bop, op, blop, lop, and, mul, red, get1, get2, put}. Стоимостные характеристики процесса определяются с использованием функций, которые вычисляют стоимость выполнения i-й операцией k-го заказа (k≥0). Каждой единице из множества E соответствует своя функция. Стоимость операции обозначим как gie,, где i – номер операции, а e – тип оборудования из множества E=(e1,e2…em), на котором может выполнятся данная операция. Каждая операция может выполнять только один заказ, и каждая единица оборудования может выполнять только одну операцию.
V). Вершины графа представляют собой операцию производственного процесса, либо спусковую функцию, определяющую временное предшествование операций. Для определения типа вершины отметим их как отображение type: V→O, где O – множество вида {bop, op, blop, lop, and, mul, red, get1, get2, put}. Стоимостные характеристики процесса определяются с использованием функций, которые вычисляют стоимость выполнения i-й операцией k-го заказа (k≥0). Каждой единице из множества E соответствует своя функция. Стоимость операции обозначим как gie,, где i – номер операции, а e – тип оборудования из множества E=(e1,e2…em), на котором может выполнятся данная операция. Каждая операция может выполнять только один заказ, и каждая единица оборудования может выполнять только одну операцию.
Определим функцию c(i,k), которая обращается к одной из единиц множества O, в соответствии с типом вершины.

В зависимости от типа, вершины могут иметь одну или две входных дуги. Переходы между вершинами выполняются с помощью функций вида:
pred(i)- считает номер j вершины, при том, что есть дуга ![]() ;
;
pred1(i)-считает номер p 1-й вершины, с условием, что есть дуга ![]() ;
;
pred2(i)- считает номер q 2-й вершины, с условием, что есть дуга ![]() .
.
Стоимость операции вычисляется поэлементным методом:
![]()
где:
M – расходы на материалы;
Зо – зарплата;
Зв – зарплата наладчиков;![]()
Аотч – амортизация;
Sин - расходы на инструменты;
Sос – затраты на расходную оснастку;
Sэ – электроэнергия;
Sр – работы по ремонту;
Sн – настройка оборудования;
Пр – прочие расходы.
Опишем вершины графа, их графическое отображение и смысловое содержание:
- Начальная операция
Является начальной производственной операцией, характеризуется стоимостью gie. Стоимость выполнения i-й операции k-го заказа c(i,k) рассчитывается как стоимость выполнения самой операции gie. (Рис. 1).

Рисунок 1. Начальная операция
- Производственная операция
Производственная операция (не начальная) так же характеризуется стоимостью выполнения, которая рассчитывается как сумма i-й операции k-1 заказа плюс стоимость операции c(j,k) и плюс стоимость самой операции gie, если k>0 и i=n. Если k=0 и i=n, то стоимость i-й операции k-1 заказа равняется стоимости предыдущей операции плюс стоимость самой операции gie,. Если 0≤i<n и k≥0, то стоимость рассчитывается как и в предыдущем случае. n – завершающая операция конвейера (Рис. 2).

Рисунок 2. Производственная операция
- Линейный конвейер.
Линейный конвейер в отличии от обычной операции, в стоимость нулевого заказа включает единовременные затраты, такие как – расходы на инструмент (Sин), расходы на настройку оборудования (Sн). Все последующие обработки заказов операцией не учитывают вышеперечисленные расходы, и вычисляются как стоимость выполнения i-й операции k-го заказа c(i,k) рассчитывается как стоимость операции gie. плюс стоимость выполнения k-1-го заказа (Рис. 3).

Рисунок 3. Начальный линейный конвейер
Линейный конвейер (для k≥1) также характеризуется стоимостью выполнения, которая рассчитывается как сумма i-й операции k-1 заказа плюс стоимость операции c(j,k), плюс стоимость самой операции gie ,если k>0 и i=n. Если k=0 и i=n, то стоимость i-й операции k-1 заказа равняется стоимости предыдущей операции плюс Ci. Если 0≤i<n и k≥0, то стоимость рассчитывается как стоимость предшествующей c(j,k) операции плюс стоимость самой операции gie (Рис. 4).
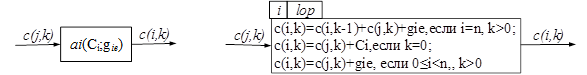
Рисунок 4. Линейный конвейер
- Функция and
Функция рассчитывает стоимость k-го заказа путем суммирования стоимости двух операций, являющимися предшествующими i (pred(i)) т.е. (c(p,k) и c(q,k)) (Рис.5).
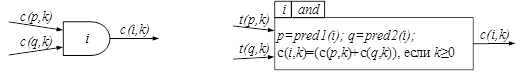
Рисунок 5. Функция and
- Функция мультиплицирования
Данная функция при каждом завершении операции j, выполняет q раз операцию i. Для расчета стоимости c(i,k) вычисляется k-й цикл операции j путем деления k-го цикл операции j на количество выполнений q, если (k mod q)=0. Здесь мод mod- это остаток от деления. Если (k mod q)>0, то стоимость i-й операции равняется нулю (Рис.6).
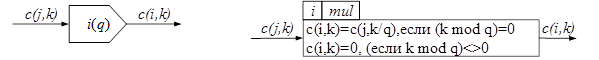
Рисунок 6. Функция mul
- Функция редуцирования
Данная функция на одно завершение операции i, производит q выполнений операции j. Для расчета стоимости c(i,k) вычисляется k-й цикл операции j путем умножения k-го цикл операции j на количество выполнений q, плюс k-й цикл операции j умноженный на количество повторений q плюс один, суммирование продолжается до тех пор пока алгоритм не дойдет до требуемого количества повторений q минус 1 (Рис.7).

Рисунок 7. Функция red
- Функция раздачи
Функция get воспроизводит реальную производственную ситуацию, когда после выполнения операции, произведенное изделие по четным циклам отправляется на конвейер, соответствующий функции get1, а по нечётным – get2 (Рис.8).

Рисунок 8. Функция get
- Функция приема
Функция соединяет две операции для выполнения третий (Рис.9). Как и функция and, она суммирует стоимость выполнения двух предшествующих операций.
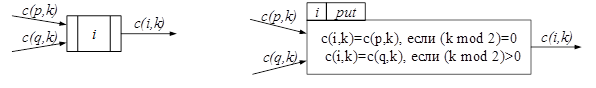
Рисунок 9. Функция put
Рассмотрим пример модели конвейера (Рис.10) и вычислим стоимостные характеристики.
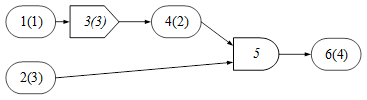
Рисунок 10. Пример модели конвейера
Вычисление стоимости процесса осуществляется следующим образом:
С(6,4)=С(6,3)+C(5,4)+4=38+5+4=47 // Расчет производится рекурсивно - с последней операции (6,4), стоимость которой равняется стоимости шестой операции предыдущего цикла (С(6,3)) полюс стоимость предшествующей операции С(5,4) и плюс стоимость самой операции (4).
C(6,3) = С(6,2)+C(5,3)+4=28+6+4=38 // На каждой итерации уменьшаем цикл на 1, дальше действуем в соответствии с формулой для производственной операции.
C(6,2) = С(6,1)+C(5,2)+4=19+5+4=28
C(6,1) = С(6,0)+C(5,1)+4=10+5+4=19
C(6,0) = C(5,0)+4=10
C(5,4)= C(4,4)+C(2,4)=2+3=5 // Переходим к расчету пятой операции. Расчет производится в соответствии с формулой соответствующей спусковой функции and
C(5,2)= C(4,2)+C(2,2)=2+3=5
C(5,1)= C(4,1)+C(2,1)=2+3=5
C(5,0)= C(4,0)+C(2,0)=3+3=6
C(5,3)= C(4,3)+C(2,3)=3+3=6
C(4,4)=C(3,4)+2 =2 // Стоимость четвертой операции равняется стоимость предшествующей операции (которая является спусковой функцией) плюс стоимость выполнения самой операции.
C(4,3)=C(3,3)+2 =3
C(4,2)=C(3,2)+2 =2
C(4,1)=C(3,1)+2 =2
C(4,0)=C(3,0)+2 =3
C(3,4)=0 // Данная операция является спусковой функцией mul. В данном случае остаток от деления цикла на кол-во выполнений (4/3) равняется 33, следовательно, в соответствии с формулой, данный такт пропускается и стоимость выполнения равна нулю.
C(3,3)=C(1,1)=1 // В данном случае остаток от деления цикла на кол-во выполнений (3/3) равняется 0, следовательно, в соответствии с формулой, рассчитывается делением предыдущей операции на количество выполнений.
C(3,2)=0
C(3,1)=0
C(3,0)=C(1,0)=1
C(2,4)= 3
C(2,3)= 3
C(2,2)= 3
C(2,1)=3
C(2,0)=3
C(1,1)=1
C(1,0)=1 // Стоимость каждой операции рассчитана. Далее подставим вычисленные значения и просуммируем стоимости выполнения операций, начиная с первой операции.

