СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПРОИЗВОДИТЕЛЬНОСТИ АЛГОРИТМОВ СОРТИРОВКИ: ПУЗЫРЬКОВАЯ СОРТИРОВКА, БЫСТРАЯ СОРТИРОВКА И СОРТИРОВКА СЛИЯНИЕМ

Введение

Современные информационные системы требуют эффективных алгоритмов для обработки данных, объемы которых постоянно растут. По данным аналитических агентств, объем мировых данных к 2025 году может превысить 175 зеттабайт, что подчеркивает важность выбора подходящих алгоритмических решений. Одной из ключевых операций в таких системах является сортировка, которая используется для упорядочивания данных в базах данных, поисковых системах, аналитических платформах и других приложениях.

Выбор подходящего алгоритма сортировки существенно влияет на производительность системы. В данной статье рассматриваются три классических алгоритма: пузырьковая сортировка (Bubble Sort), быстрая сортировка (Quick Sort) и сортировка слиянием (Merge Sort). Эти алгоритмы выбраны благодаря их широкой известности, различиям в подходах к реализации и применимости к разным задачам.

Цель исследования — провести сравнительный анализ указанных алгоритмов с точки зрения временной сложности, затрат памяти и практической эффективности. Для достижения этой цели применены теоретические оценки производительности, основанные на O-нотации, и экспериментальная проверка на случайных наборах данных. Работа опирается на фундаментальные труды в области алгоритмов [1;3], что обеспечивает надежную основу для выводов.

Теоретические основы

Пузырьковая сортировка

Пузырьковая сортировка — это простой и интуитивно понятный алгоритм, который многократно проходит по массиву, сравнивая соседние элементы и обменивая их местами, если они находятся в неправильном порядке. Процесс напоминает "всплывание" больших элементов к концу массива, отсюда и название [2]. Алгоритм завершает работу, когда за проход не происходит обменов.

Временная сложность пузырьковой сортировки составляет O(n²) в худшем и среднем случае, где n — число элементов массива. В лучшем случае (почти отсортированный массив) сложность снижается до O(n), но это редкий сценарий [1]. Алгоритм не требует дополнительной памяти, кроме нескольких переменных, что делает его экономичным с точки зрения пространства (O(1)). Однако из-за квадратичной зависимости времени выполнения он становится непрактичным для больших данных [3].

Быстрая сортировка

Быстрая сортировка, разработанная Тони Хоаром в 1960 году, относится к классу алгоритмов "разделяй и властвуй". Она начинается с выбора опорного элемента (pivot), вокруг которого массив делится на две части: элементы меньше опорного и элементы больше или равные ему. Затем процесс рекурсивно применяется к каждой из частей [1].

Средняя временная сложность быстрой сортировки составляет O(n log n), что делает ее одной из самых эффективных для общего применения. Однако в худшем случае (например, при выборе неудачного опорного элемента в отсортированном массиве) сложность возрастает до O(n²). Выбор опорного элемента критически влияет на производительность: случайный выбор или медиана из трех значений снижают вероятность худшего случая [3]. Пространственная сложность зависит от глубины рекурсии и в среднем составляет O(log n) за счет стека вызовов [1].

Сортировка слиянием

Сортировка слиянием также использует стратегию "разделяй и властвуй". Алгоритм делит массив пополам до тех пор, пока не останутся подмассивы из одного элемента, а затем сливает их в отсортированные последовательности. Процесс слияния требует сравнения элементов из двух подмассивов и их объединения в новый массив [4].

Временная сложность сортировки слиянием всегда равна O(n log n), что обеспечивает стабильную производительность независимо от структуры входных данных. Однако алгоритм требует дополнительной памяти O(n) для хранения временных массивов во время слияния, что может быть недостатком при ограниченных ресурсах [1]. Сортировка слиянием устойчива, то есть сохраняет порядок равных элементов, что важно для некоторых приложений [4].

Методика анализа

Анализ проводился в два этапа: теоретический и экспериментальный.

1. Теоретическая оценка: на основе литературы определены временная и пространственная сложность алгоритмов. Использовались стандартные метрики: O-нотация для времени и объема памяти [1;3]. Особое внимание уделено факторам, влияющим на производительность, таким как выбор опорного элемента в быстрой сортировке и структура данных в сортировке слиянием.
2. Экспериментальная проверка: алгоритмы реализованы на языке Python версии 3.10. Для замера времени использовалась функция time.time(), а для генерации случайных массивов — модуль random. Тестирование проводилось на массивах размером 1000, 5000, 10000 и 20000 элементов. Каждый алгоритм запускался 10 раз на каждом наборе данных, после чего вычислялось среднее время выполнения.

Результаты представлены в Таблице 1 (среднее время выполнения в секундах) и на Рисунке 1 (график зависимости времени от размера массива). Графики созданы с помощью библиотеки matplotlib и сохранены в формате jpg, обеспечивая читаемость в черно-белом виде. Для оценки повторяемости эксперимента использовались массивы с равномерным распределением значений от 0 до 100000.

Таблица 1.

Среднее время выполнения алгоритмов (с)

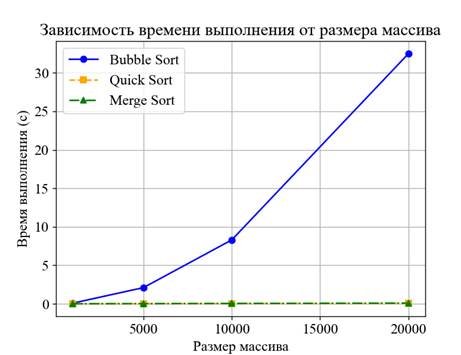
Рисунок 1. График зависимости времени от размера массива

Результаты

Таблица 1 демонстрирует значительные различия в производительности алгоритмов.

Пузырьковая сортировка показала худшие результаты: для массива из 20000 элементов среднее время выполнения составило 32,5 секунды. Быстрая сортировка справилась с тем же массивом за 0,05 секунды, а сортировка слиянием — за 0,09 секунды. Эти данные подтверждают теоретические оценки: квадратичная сложность O(n²) делает пузырьковую сортировку непригодной для больших объемов данных [2].

Рисунок 1 иллюстрирует зависимость времени выполнения от размера массива. Кривая пузырьковой сортировки имеет выраженный квадратичный рост, тогда как быстрая сортировка и сортировка слиянием демонстрируют почти линейный рост с логарифмическим коэффициентом, что соответствует O(n log n). Разница между быстрой сортировкой и сортировкой слиянием объясняется меньшими накладными расходами первой на операции с памятью [1].

Интересно отметить, что в экспериментах с массивами до 1000 элементов различия между алгоритмами менее заметны: пузырьковая сортировка занимает 0,08 секунды, быстрая — 0,001 секунды, а слиянием — 0,003 секунды. Это указывает на то, что для малых данных накладные расходы на рекурсию и выделение памяти могут перевешивать преимущества более сложных алгоритмов [4].

Быстрая сортировка показала себя как наиболее эффективный алгоритм в среднем случае благодаря оптимизации выбора опорного элемента (в данном случае использовалась медиана из первого, среднего и последнего элементов). Однако в редких случаях (например, при почти отсортированных данных) ее производительность ухудшалась, что согласуется с выводами Кнута [3]. Сортировка слиянием, напротив, сохраняет стабильность и предсказуемость, что делает ее предпочтительной для задач с жесткими требованиями к времени выполнения.

Таким образом, выбор алгоритма сортировки зависит от размера данных и требований к производительности. Быстрая сортировка оптимальна в среднем случае, а сортировка слиянием — в ситуациях, где важна стабильность. Пузырьковая сортировка может быть оправдана только для небольших массивов или в образовательных целях [2].

Заключение

Проведенное исследование подтвердило, что выбор алгоритма сортировки существенно влияет на эффективность обработки данных. Пузырьковая сортировка с временной сложностью O(n²) демонстрирует низкую производительность и подходит только для малых объемов данных. Быстрая сортировка и сортировка слиянием, обе с O(n log n), являются более эффективными решениями. Быстрая сортировка выигрывает по скорости в среднем случае, тогда как сортировка слиянием обеспечивает стабильность и предсказуемость за счет дополнительных затрат памяти.

Полученные результаты имеют практическое значение для разработчиков программного обеспечения, работающих с задачами сортировки. В качестве направлений дальнейших исследований можно рассмотреть адаптацию этих алгоритмов для параллельных вычислений или их модификацию для работы с данными, хранящимися на внешних носителях. Также интерес представляет изучение влияния структуры данных (например, частичная упорядоченность) на производительность алгоритмов.