НЕЙРОСЕТЕВЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОММИВОЯЖЕРА
Журнал: Научный журнал «Студенческий форум» выпуск №39(306)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №39(306)
НЕЙРОСЕТЕВЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОММИВОЯЖЕРА
Аннотация. Задача коммивояжера или (Travelling Salesman Problem) является NP-полной задачей в области комбинаторной оптимизации. Для задачи TSP не существует алгоритма способного найти оптимальное решение за полиномиальное время. В данной статье рассматриваются нейросетевые методы решения задачи коммивояжера, включая нейронную сеть Хопфилда, графовую нейронную сеть и нейронную сеть с подкреплением.
Ключевые слова: задача коммивояжера; нейронная сеть Хопфилда; графовая нейронная сеть; нейронная сеть с подкреплением.
Hopfield neural network
Сеть Хопфилда является рекуррентной нейронной сетью, где каждый нейрон связан с каждым другим. Пусть N — количество нейронов в сети, а ![]() — вектор состояния нейронов, где
— вектор состояния нейронов, где ![]() . Матрица весов связей между нейронами обозначается как
. Матрица весов связей между нейронами обозначается как ![]() , где
, где ![]() — вес связи между нейронами i и j.
— вес связи между нейронами i и j.
Состояние нейрона ![]() обновляется по следующему правилу:
обновляется по следующему правилу: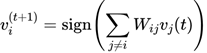
где ![]() — функция знака, возвращает 1, если
— функция знака, возвращает 1, если ![]() , и −1, если
, и −1, если ![]() .
.
Матрица весов![]() определяется на основе сохраненных паттернов. Если
определяется на основе сохраненных паттернов. Если ![]() — k-й паттерн, то:
— k-й паттерн, то:
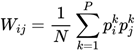
где P — количество паттернов.
Сеть Хопфилда действует как ассоциативная память, восстанавливая сохраненные паттерны из неполных или искаженных данных.
Neural network with reinforcement learning
В нейронных сетях с подкреплением используется концепция
наличия агентов – свободных акторов системы, которые могу выбирать свои оптимальные стратегии в зависимости от математической модели. Агенты взаимодействуют с окружающей средой и получает вознаграждения или наказания, чтобы обучиться оптимальной стратегии. Пусть s – состояние среды, а – действие, R - функция вознаграждения (критерий оптимальности).
Основное уравнение оптимальности – уравнение Беллмана:
![]()
где ![]() – функция ценности действия a в состоянии s, γ – коэффициент дисконтирования.
– функция ценности действия a в состоянии s, γ – коэффициент дисконтирования.
Нейронная сеть может использоваться для аппроксимации функции ценности QQQ, и обучается с использованием градиентного спуска, чтобы минимизировать ошибку между предсказанными и реальными значениями
![]()
Graph neural network
Графовые нейронные сети обрабатывают данные в виде графов ![]() , где
, где ![]() ,
, ![]() . Пусть
. Пусть ![]() — вектор признаков узла i, а
— вектор признаков узла i, а ![]() — матрица смежности графа. Для агрегации информации из соседних узлов используется следующая формула обновления:
— матрица смежности графа. Для агрегации информации из соседних узлов используется следующая формула обновления:
![]() где
где ![]() множество соседей узла i, а Aggregation может быть любой функцией агрегации. После агрегации применяется функция обновления весов.
множество соседей узла i, а Aggregation может быть любой функцией агрегации. После агрегации применяется функция обновления весов.
![]()
Для графа G=(V,E)G = (V, E)G=(V,E), где {V} — множество вершин, а {E} — множество рёбер, задача коммивояжёра заключается в нахождении кратчайшего замкнутого пути, который проходит через каждую вершину ровно один раз и возвращается в исходную вершину. Формулировка задачи включает следующие элементы:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]()
![]() (4)
(4)
Формально задача может быть представлена как задача целочисленного программирования, где переменные ![]() указывают на то, используется ли ребро (i,j)(i, j)(i,j) в пути.
указывают на то, используется ли ребро (i,j)(i, j)(i,j) в пути.
Уравнения (2) и (3) гарантируют, что в цикле будет только одна вершина графа в качестве начальной и одна в качестве конечной, а уравнение (4) обеспечивает отсутствие решений являющихся замкнутыми циклами, что гарантирует обход всех точек.
В работе Ma и др. [4] был использован графовый указатель, предложенный Vinyals, который обучался с помощью методов подкрепляющего обучения для оптимизации иерархической стратегии и механизма вознаграждения. Bello [5] также обучил графовый указатель с отрицательной длиной пути в качестве сигнала вознаграждения и применил метод градиентного спуска для оптимизации параметров рекуррентной нейронной сети. Deudon и др. [6] заменили LSTM в методе Bello и совместили его с эвристикой 2-opt, что позволило получить более удовлетворительные результаты при применении к задаче коммивояжера.
Кроме использования графовых указателей в сочетании с обучением с подкреплением, предложены и другие сети и системы для решения данной задачи. В частности, Dai и др. [7] применили архитектуру Structure2Vec для встраивания вершин графа в информационные признаки и использовали Q-обучение вместе с жадным методом вставки для размещения каждой новой вершины в локально оптимальную позицию в частично сформированном маршруте, таким образом постепенно формируя тур. Bresson [8] применил фреймворк трансформера для кодирования, обучал его с помощью подкрепляющего обучения и декодировал с помощью поиска по лучу. Решение на основе трансформера показал лучшие результаты по сравнению с ранее предложенными методами решения задачи коммивояжера.
Выводы
Сложность графовых данных представляет собой серьезный вызов для дальнейших исследований, поскольку графовые структуры имеют высокую степень связности и множество параметров, что усложняет задачу их обработки и анализа.
Хотя графовые нейронные сети (GNN) демонстрируют высокую эффективность в решении TSP, необходимо исследовать их способность к решению других комбинаторных задач. Генерализационная способность этих сетей, то есть их возможность справляться с различными задачами оптимизации, остается открытым вопросом и требует дальнейшего изучения. Использование больших языковых моделей (LLM) для решения комбинаторных задач, таких как TSP, также представляет перспективное направление. LLM, такие как GPT-2 и выше, могут эффективно обрабатывать сложные и разнообразные данные, предоставляя мощные инструменты для моделирования и предсказания. Однако, необходимо учитывать высокие требования к вычислительным ресурсам и сложность интерпретации решений, что может быть предметом дальнейших исследований и улучшений.
В целом, для достижения оптимальных результатов в решении TSP важно учитывать конкретные требования задачи, доступные ресурсы и необходимый уровень точности решения. Комбинирование различных методов и разработка гибридных подходов могут способствовать преодолению существующих ограничений и улучшению эффективности решений. Интеграция новых технологий и алгоритмов в существующие модели может открыть новые перспективы и улучшить производительность в решении задач комбинаторной оптимизации.

