РОМБЫЛЫҚ АНИЗАТРОПИЯ ТОЛҚЫН ӨТКІЗГІШІНІҢ (Х, У) ЖАЗЫҚТЫҒЫНДАҒЫ TE ПОЛЯРИЗАЦИЯСЫНЫҢ ТОЛҚЫН ДИСПЕРСИЯСЫ
Журнал: Научный журнал «Студенческий форум» выпуск №22(201)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №22(201)
РОМБЫЛЫҚ АНИЗАТРОПИЯ ТОЛҚЫН ӨТКІЗГІШІНІҢ (Х, У) ЖАЗЫҚТЫҒЫНДАҒЫ TE ПОЛЯРИЗАЦИЯСЫНЫҢ ТОЛҚЫН ДИСПЕРСИЯСЫ
ДИСПЕРСИЯ ВОЛН ТЕ ПОЛЯРИЗАЦИИ В ПЛОСКОСТИ (Х, У) В ВОЛНОВОДЕ РОМБИЧЕСКОЙ АНИЗОТРОПИИ
Маратов Сунгат
магистрант, кафедра Техническая физика, Евразийский национальный университет имени Л.Н. Гумилева, РК, г. Нур –Султан
Тлеукенов С.К.
научный руководитель, Евразийский национальный университет имени Л.Н. Гумилева, РК, г. Нур –Султан
DISPERSION OF TE POLARIZATION WAVES IN THE PLANE (X, Y) IN A RHOMBIC ANISOTROPY WAVEGUIDE
Maratov Sungat
Department of Technical Physics, L.N. Gumilyov Eurasian National University,
RK, Nur–Sultan
Tleukenov S.K.
Supervisor, Master's student, Department of Technical Physics, L.N. Gumilyov Eurasian National University, RK, Nur–Sultan
Аннотация. Бұл жұмыста біртекті, өте жақсы өткізгіш ромбтық толқын өткізгіштің қуатын сандық бағалауды есептеу үшін өлшемсіз пайдалы әсер коэффициенті қолданылады. Гельмгольц теңдеуінің бөлінбейтін шешімдерінің шексіз қосындысын қамтитын жаңа әдіс тиімділікті есептеу кезінде қолданылатын нақты функциялар мен меншікті мәндерді қамтамасыз етеді. Ромб толқын өткізгіштің қуаты стандартты тікбұрышты толқын өткізгіштің қуатымен салыстырылады және сәл төменірек болады.
Аннотация. В данной работе используется безразмерный коэффициент полезного действия для вычисления количественной оценки мощности однородного, идеально проводящего ромбического волновода. Новый метод, включающий бесконечную сумму неразделимых решений уравнения Гельмгольца, обеспечивает точные собственные функции и собственные значения для использования при расчете коэффициента полезного действия. Мощность ромбического волновода сравнивается с мощностью стандартного прямоугольного волновода и оказывается лишь немного ниже.
Abstract. Abstract -In this paper, a dimensionless efficiency coefficient is used to calculate a quantitative estimate of the power of a homogeneous, ideally conducting rhombic waveguide. The new method, which includes an infinite sum of inseparable solutions of the Helmholtz equation, provides accurate eigenfunctions and eigenvalues for use in calculating the efficiency. The power of a rhombic waveguide is compared with the power of a standard rectangular waveguide and turns out to be only slightly lower.
Кілт сөздер: пайдалы әсер коэффициенті, ромбтық толқын өткізгіш, TE және TM поляризация, дисперсия.
Ключевые слова: коэффициент полезного действия, ромбический волновод, TE и TM поляризаций, дисперсия.
Keywords: efficiency, rhombic waveguide, TE and TM polarizations, dispersion.
Периодты құрылымдардың моделдері қатты денелер физикасы,физикалық электроника,оптикалық жүйелерде кеңінен қолданылады және де әртүрлі приборлар мен құрылғылар жасаудың негізі болады.
Матрицант құрылымы деген түсінікті енгізу және анықтау, Бриллюэн мен Парод[5] дамытқан тұтас периодты біртекті емес ортадағы дискретті периодты құрылымдар үшін арналған классикалық әдіс кеңінен тарады. Толқындардың қабаттарда таралуы толқынжолдағы толқындық процесстерге жатады.Толқынжолдар радиотехникалық,радиолокациялық және электрондық құрылғылар мен приборлада кеңінен қолданылады. Чебышев-Гегенбауэрдың үзіліссіз біртекті емес периодты ортадағы полиномдары [90] монография мен [102] жұмыстарда кеңінен қолданылды. Электромагнитті толқын кездегі периодты біртекті емес анизотропты орта, кеңістіктік координаталардың периодтық функцияларымен сипатталады және мына шарттарды қанағаттандырады
![]() ,
,
![]() (1)
(1)
h- біртекті еместіктің периоды(период неоднородности)
Шектелмеген периодты құрылымдағы электромагнитті толқындық процесстердің заңдылығын сипаттайтын – дисперсия.Матрицанттың құрылымы тривиалды емес шешімдердің болу шартын өзгерте алады және сипаттамалық теңдеудің дәрежесін екі есе төмендетеді.
x осіне бағытталған, қабатта таралатын TE поляризацияланған электромагниттік толқын дисперсиясының заңдылықтары зерттелуде. ![]() толқындық векторы x,z жазықтықтарында орналасқан.
толқындық векторы x,z жазықтықтарында орналасқан.
- анизотроптық қабаттағы толқын жылдамдықтарының дисперсия заңдылықтары изотроптық қабаттағы толқындардың дисперсиясына сәйкес келеді;
- анизотроптық қабаттағы жылдамдықтардың мәнін материалды параметрлердің үлкен саны анықтайды.
![]() , өзек радиусы a = 1, өзектегі салыстырмалы диэлектрлік тұрақтылық ε1 = 2.56, қабатта ε2 = 1.536 деп алдық. Есептеулер үш торда жүргізілді. 5 максималды меншікті мән анықталды. Формуламен негізгі шешімдер есептелді және басқа режимдерге сәйкестігі анықталды (мода q айналмалы нөмірімен және түбір нөмірімен есептеледі). 2 – 4 - де табылған нәтижелер бейнеленген, олардан торды майдалау әдісі арқылы меншікті мәндердің конвергенциясы байқалады.
, өзек радиусы a = 1, өзектегі салыстырмалы диэлектрлік тұрақтылық ε1 = 2.56, қабатта ε2 = 1.536 деп алдық. Есептеулер үш торда жүргізілді. 5 максималды меншікті мән анықталды. Формуламен негізгі шешімдер есептелді және басқа режимдерге сәйкестігі анықталды (мода q айналмалы нөмірімен және түбір нөмірімен есептеледі). 2 – 4 - де табылған нәтижелер бейнеленген, олардан торды майдалау әдісі арқылы меншікті мәндердің конвергенциясы байқалады.
Кесте 1.
792 қабырғадан тұратын тордағы шешім
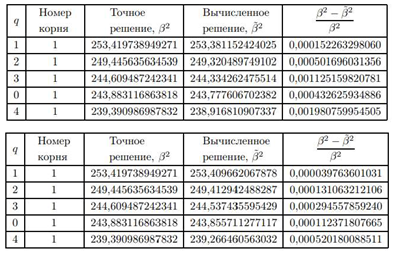
Кесте 2.
12 540 қабырғадан тұратын тордағы шешім
Трансляцияланған симметрия кезде Блох теормесынан [5, 11] шығады:
![]() , (2)
, (2)
![]() - баған вектор,мына теңдеудің шешімі
- баған вектор,мына теңдеудің шешімі
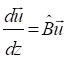 . (3)
. (3)
h біртекті еместіктің периоды үшін арналған (10.1.3) теңдеудің матрицанты монодромияның матрицасына жатады.Соған сәйкес алатынымыз:
![]() ,
, ![]() (4)
(4)
(10.1.2) мен (10.1.4) – ті біріктіріп алатынымыз:
![]()
![]() (5)
(5)
I – бірлік матрица.Мына шарттан
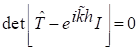 (6)
(6)
сипаттамалық теңдеу шығады,оның түбірлері шектелмеген периодтық құрылымдағы толқын дисперсиясының теңдеуін анықтайды.
(10.1.5) – ті ![]() -ке көбейткенде мына теңдеу шығады
-ке көбейткенде мына теңдеу шығады
![]() ;
; ![]() (7)
(7)
(10.1.5) мен (10.1.7) қатынастары эквивалентті,екеуі де бір спектрді анықтайды.Физикалық түрде бұл теріс бағытта шектелмеген периодты құрылымда таралатын толқындар үшін дисперсия заңы біреу дегенді білдіреді.Осы қатынастарды біріктіріп, тривиалды емес шешімдердің болу шартының мынандай модификацияланған формасына келеміз:
![]() . (8)
. (8)
(10.1.8) – ші шартта тұрақты құрылымдар үшін өте маңызды және әрі қарай кеңінен қолданылатын матрица енгізілген
![]() . (9)
. (9)
Бірақ (10.1.9) жалғыз форма емес,онымен бірге мына матрицаны енгізуге болады:
![]() . (10)
. (10)
(10.1.10) – нан тривиялды емес шешімдердің болу шартының мынандай формасы шығады
![]() . (11)
. (11)
Шектелмеген ортада таралатын тура және кері толқындардың симметриялы болуына байланысты ![]() түрлі матрицасы (10.1.9) бар (10.1.8) – ші форма, (10.1.11) – ші формаға қарағанда қосымшада (приложение) қолданылуға ыңғайлы.Әрі қарай (10.1.8) – ші форма негізінде дисперсия теңдеуінің шешімі талқылануда.
түрлі матрицасы (10.1.9) бар (10.1.8) – ші форма, (10.1.11) – ші формаға қарағанда қосымшада (приложение) қолданылуға ыңғайлы.Әрі қарай (10.1.8) – ші форма негізінде дисперсия теңдеуінің шешімі талқылануда.
Электромагнитті толқындардың бірөлшемді таралуы кезінде және де TM мен TE толқындардың тәуелсіз,өзара трансформация болмау кезінде монодромияның тура және кері матрицасы мынандай түрде болады:
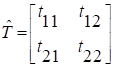 ,
, 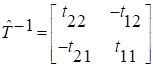 . (12)
. (12)
(10.1.12) мен (10.1.8) – і ескере отырып
![]() (13)
(13)
шығады, ![]() матрицасының түрі:
матрицасының түрі:
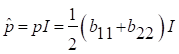 (14)
(14)
(10.1.13) дисперсия теңдеуі (10.1.14) – ке негізделіп былай жазылса болады:
![]() (15)
(15)

