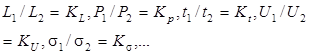Физическое моделирование конструкционных задач механики
Журнал: Научный журнал «Студенческий форум» выпуск №23(116)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №23(116)
Физическое моделирование конструкционных задач механики
PHYSICAL MODELING OF STRUCTURAL PROBLEMS IN MECHANICS
Alena Zvereva
Student, Togliatti state University, Russia, Togliatti
Vadim Gulyaev
Candidate of Science, associate Professor, Togliatti state University, Russia, Togliatti
Аннотация. В данной статье рассматриваются вопросы подобия и условия математического моделирования краевых задач при работе фрикционной системы. В механике деформируемого твердого тела метод физического и математического моделирования, наряду с численными способами, может служить как для оценки адекватности теоретических решений, так и иметь самостоятельное научное значение.
Abstract. This article discusses the similarity and conditions of mathematical modeling of boundary value problems in the operation of a friction system. In the mechanics of a deformable solid, the method of physical and mathematical modeling, along with numerical methods, can serve both to assess the adequacy of theoretical solutions, and have an independent scientific value.
Ключевые слова: математическое моделирование, физическое моделирование, методы анализа размерностей и подобия, контактирующие поверхности элементов конструкции.
Keywords: mathematical modeling, physical modeling, methods for analyzing dimensions and similarity, contacting surfaces of structural elements.
Теоретической основой физического моделирования являются методы анализа размерностей и подобия. В механике деформируемого твердого тела моделирование применяется, в основном, при экспериментальных исследованиях полей напряжений, деформаций и перемещений, возникающих под нагрузкой в модели, геометрически подобной реальному элементу в натуре (прототипу). При этой зависимости, необходимые для пересчета сходственных величин компонентов тензоров напряжения sij деформации eij (i, j=1,2,3) и вектора перемещения ui с модели («М») на натуру («Н») устанавливаются методами размерности и подобия.
Все уравнения механики деформируемого твердого тела и граничные условия являются взаимосвязями различных размерных величин, которые могут быть представлены в разных системах единиц измерения.
Правила образования формул размерности вторичных величин через размерность первичных величин предопределяют общий вид этих формул. Все они представляют собой простые степенные комплексы - одночлены в общем виде:
|
|
(1) |
где [x] - символ для обозначения размерности величины X введенный Максвелом; x - физическая величина; ai – единицы измерения основных физических величин; a1, a2… an - показатели степени.
Функции, удовлетворяющие условию
|
|
(2) |
называют гомогенными [1]. Постулат о гомогенности функций будучи фундаментальным в анализе размерностей являются основополагающим и в теории подобия, основанной на рассмотрении непрерывных групп преобразований открытых С.Ли. Одночленные степенные функции и формулы размерности обладают свойством гомогенности, также как суммы степенных комплексов одинаковой размерности и трансцендентные функции, если их аргумент представляет собой безразмерную однородную функцию вида: ![]() .
.
Систему уравнений, определяющую постановку задачи механики деформируемого твердого тела, можно представить как соотношения безразмерных величин.
Число безразмерных комплексов и симплексов равно разности N-k, а количество безразмерных комплексов ![]() равно
равно ![]() . В соответствии с этим число безразмерных комплексов является наименьшим числом безразмерных комплексов, которые можно получить из величин, входящих в исходное уравнение. Очевидно, что наименьшее число симплексов, которые можно получить из рассматриваемых величин, равно нулю, а наибольшее число комплексов равно N-k [2, 3].
. В соответствии с этим число безразмерных комплексов является наименьшим числом безразмерных комплексов, которые можно получить из величин, входящих в исходное уравнение. Очевидно, что наименьшее число симплексов, которые можно получить из рассматриваемых величин, равно нулю, а наибольшее число комплексов равно N-k [2, 3].
Несмотря на столь обширную область приложения этого метода исследований, он ограничен, так как не позволяет определить необходимые данные для этого метода - перечень существенных физических величин, включая одну зависимую и достаточное число независимых физических величин. Для практического применения ![]() - теоремы, с целью образования безразмерных комплексов и уменьшения числа независимых параметров, используют как математические способы матричного исчисления, так и эвристические методы фракционного анализа. Лишь с помощью анализа размерностей можно эффективно рассмотреть размерности, их однородность, свойства гомогенности функций и другие основные понятия, используемые при математическом описании физических процессов.
- теоремы, с целью образования безразмерных комплексов и уменьшения числа независимых параметров, используют как математические способы матричного исчисления, так и эвристические методы фракционного анализа. Лишь с помощью анализа размерностей можно эффективно рассмотреть размерности, их однородность, свойства гомогенности функций и другие основные понятия, используемые при математическом описании физических процессов.
Анализ размерностей позволяет установить список основных безразмерных комплексов ![]() , но не позволяет выявить перечень всех физических величин, характеризующих постановку исследуемой задачи. Недостатки анализа размерностей компенсируются применением теории подобия.
, но не позволяет выявить перечень всех физических величин, характеризующих постановку исследуемой задачи. Недостатки анализа размерностей компенсируются применением теории подобия.
В зависимости от вида соответствующей группы непрерывного преобразования, между сходственными величинами двух систем, переводящего их из одной системы в другую, в механике деформируемого твердого тела используются разновидности подобия. Так, например, две фигуры (тела) геометрически подобны, если существует преобразование подобия, переводящее одну из них в другую. В математике подобие обозначают знаком ~ и термином idem.
Два физических явления подобны, если численные значения всех величин, характеризующих первое явление в одной системе (например, силы, скорости, промежутки времени, длины, напряжения, деформации, перемещения и т.д.), могут быть получены в другой системе путем умножения соответствующих величин на постоянные безразмерные множители (масштабы подобия). Эти множители в общем случае различны для разных величин, но все одноименные величины в соответственных точках обеих систем и (если явления неустановившиеся) в соответственные моменты времени имеют одинаковые масштабы подобия, а масштабы подобия безразмерных величин (углов, коэффициентов Пуассона и т.п.) равны единице. Следовательно, при простом подобии двух явлений имеют место соотношения
|
|
(3) |
В (3) ![]() - физические величины: длина, сила, время, скорость, напряжение; K - коэффициенты пропорциональности (сомножители), являющиеся константами подобия и представляющие собой масштабы соответствующих величин.
- физические величины: длина, сила, время, скорость, напряжение; K - коэффициенты пропорциональности (сомножители), являющиеся константами подобия и представляющие собой масштабы соответствующих величин.
Подобие явлений обусловлено, прежде всего, их геометрическим подобием. В исследовании подобных фигур основную роль играет теорема о параллельных секущих: если стороны угла пересечь параллельными прямыми, то отношение отрезков, отсеченных на одной из сторон, равно отношению соответствующих отрезков на другой стороне угла.
Геометрически подобные системы обладают следующим свойством: если в качестве масштабов выбрать сходственные геометрические параметры, то функции или уравнения, описывающие подобные геометрические системы, после приведения их путем масштабных преобразований к безразмерному виду становятся тождественными.
Приведенный подход простого подобия при физическом и математическом моделировании является универсальным и его можно отнести к любым явлениям. С помощью предлагаемого подхода можно осуществить описание поведения технических систем различного вида. К ним можно отнести следующие системы: статические, механические, кинематические, энергетические, тепловые, электрические, динамические, гидродинамические, аэродинамические, термодинамические, электродинамические и другие виды.