Расчет напряженно-деформированного состояния двухэтажного здания на основе пластинчатой континуальной модели при сейсмических воздействиях
Конференция: XXVII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Механика деформируемого твердого тела

XXVII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Расчет напряженно-деформированного состояния двухэтажного здания на основе пластинчатой континуальной модели при сейсмических воздействиях
CALCULATION OF THE STRESS-STRAIN STATE OF TWO-STORY BUILDING BASED ON THE CONTINUOUS PLATE MODEL OF BUILDINGS UNDER SEISMIC EFFECTS
Makhamatali Usarov
Doctor of physical and Mathematical Sciences, Institute of Mechanics and Seismic Stability of Structures of the Academy of Sciences of the Republic of Uzbekistan, Uzbekistan, Tashkent
Gayratjon Ayubov
Junior researcher, Institute of Mechanics and Seismic Stability of Structures of the Academy of Sciences of the Republic of Uzbekistan, Uzbekistan, Tashkent
Аннотация. В статье смоделировано движение двухэтажного здания в виде толстой анизотропной консольной пластины на основе бимоментной теории при сейсмических воздействиях. В качестве сейсмического воздействия заданы ускорение, дейстующее в виде кинематического воздействия на уровне основания здания. Приведены численные результаты задачи колебания двухэтажного здания и их анализ.
Abstract. The article simulates the movement of a two-story building in the form of a thick anisotropic cantilever plate based on the bimoment theory during seismic effects. Acceleration acting as a kinematic action at the base level of the building is specified as a seismic action. The numerical results of the oscillation problem of a two-story building and their analysis are presented.
Ключевые слова: сейсмические воздействия; континуальная пластинчатая модель здания; консольная пластина; момент; бимомент.
Keywords: seismic effects; continuum plate model of a building; cantilever plate; moment; bimoment.
Основная территория многих стран мира находится в высоко сейсмоактивных регионах, поэтому учет сейсмических воздействий при проектировании и строительстве зданий и сооружений остается актуальным вопросом. Расчетные модели зданий, сооружений и элементов конструкций должны разрабатываться с учетом реальных факторов, которые существенно влияют на их динамическое поведение и напряженно-деформированное состояние [1, 2].
В расчетах многих элементов конструкций в виде пространственных систем ячеистой структуры для описания их динамического поведения широко используется континуальное моделирование. К таким исследованиям относятся работы [3, 4], в которых выполнены расчеты в области ракетной техники.
Ряд задач о колебаниях пластинчатых и оболочечных конструкций, взаимодействующих с грунтом, как показано в [5, 6], целесообразно решать в рамках бимоментной теории. Здание, по своей геометрической структуре, является пространственным телом в форме параллелепипеда с ячеистой структурой. В качестве первого приближения расчета колебания здания можно сопоставить с колебаниями некоторого трехмерного континуального тела в виде параллелепипеда. В работах [7, 8] предложена континуальная пластинчатая модель здания в виде толстой консольной ортотропной пластины, теория которой разработана в [5, 6] без упрощающих гипотез с учетом бимоментов в рамках трехмерной динамической теории упругости. Сущность континуальной модели заключается в том, что рассматриваемое тело в форме параллелепипеда может быть заменено некоторой эквивалентной сплошной толстой пластиной с приведенными жесткостными характеристиками.
Данная статья посвящена разработке методики расчета напряженно-деформированного состояния здания с использованием пластинчатой континуальной модели здания, описывающей его сейсмические колебания. Сформулирована постановка задачи о поперечных колебаниях здания на основе пластинчатой модели, разработанной в рамках бимоментной теории. В качестве уравнения движения здания и граничных условий принимаются уравнения и граничные условия толстой консольной пластины [5,6], которые адекватно отражают пространственную форму колебаний с учетом поперечного сдвига и изгибно-продольных деформаций.
Для описания движения здания пластины введем декартовую систему координат с переменными ![]() и
и ![]() . Начало координат расположено в нижнем левом углу срединной поверхности континуальной пластины. Направим оси OX1 и OX2 по длине и высоте, а ось OZ – вдоль толщины (ширины здания) пластинчатой модели.
. Начало координат расположено в нижнем левом углу срединной поверхности континуальной пластины. Направим оси OX1 и OX2 по длине и высоте, а ось OZ – вдоль толщины (ширины здания) пластинчатой модели.
Предположим, что сейсмическое движение грунта происходит в направлении оси ОZ (ширины здания). Исходя из этого, в качестве внешнего воздействия на нижнем защемленном крае задаём ускорение основания ![]() в виде:
в виде:
![]() , (1)
, (1)
где ![]() и
и ![]() – соответственно максимальное ускорение и частота грунтового основания.
– соответственно максимальное ускорение и частота грунтового основания.
В основании здания граничные условия для изгибно-сдвиговых колебаний имеют вид:
![]() . (2)
. (2)
На свободных боковых гранях здания имеем условия равенства нулю сил, моментов и бимоментов и силовых факторов:
![]() . (3)
. (3)
На свободной верхней грани здания имеем условия:
![]() . (4)
. (4)
Задача решена методом конечных разностей. Конечно-разностные уравнения движения поперечных колебаний зданий [7, 8] имеют следующий вид:
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
где ![]() – изгибающие моменты и перерезывающие силы;
– изгибающие моменты и перерезывающие силы; ![]() – продольные бимоменты,
– продольные бимоменты, ![]() ; р33 – интенсивности поперечных бимоментов.
; р33 – интенсивности поперечных бимоментов.
Система уравнений движения относительно трех обобщенных функций ![]() аппроксимируется в виде
аппроксимируется в виде
 (9)
(9)
 (10)
(10)
Условно считаем, что механические и геометрические характеристики материалов панелей комнат одинаковые: модуль упругости E=20000 МПа, плотность ρ=2700 кг/м3 и коэффициент Пуассона ν=0.3.
Приведем результаты расчетов вынужденных колебаний здания в рамках толстой пластинчатой модели при следующих размерах плит и здания: длина и ширина здания а=30 м, H=11 м, высота одного этажа здания b1=3 м, толщины несущих внешних и внутренних стен h1=0.25 м и h2=0.2 м, толщина перекрытия hпер=0.2 м.
На основе вышеуказанных исходных данных по выражениям для определения плотности и модуля упругости пластинчатой модели здания, приведенных в [7], находим следующие характеристики материалов здания:
![]()
В расчетах коэффициент сейсмичности и частота ускорения основания заданы: kc=0.1 и ω0=9.5 Гц. Введены безразмерные переменные x=x1/a, y=x2/b, τ=ct/H, где ![]() .
.
Шаг вычисления по безразмерным координатам принят Δx=1/60, Δy=1/30. Устойчивость расчета по безразмерному времени обеспечена по явной схеме при шаге Δ=0.01.
|
а) |
б) |
|
|
|
|
Рисунок 1.Форма колебания (а) и изолинии обобщенного перемещения r двухэтажного здания в безразмерном времени τ=52.37 (б) |
|
При расчете получены максимальные перемещения в крайних точках на верхнем уровне второго этажа здания. На рисунке 1 показаны форма колебания (а) и изолинии обобщенного перемещения ![]() двухэтажного здания в безразмерном времени τ=52,37 (б).
двухэтажного здания в безразмерном времени τ=52,37 (б).
На рисунках 2-4 показаны изолинии напряжений в безразмерных значениях времени. Используя изолинии, обнаружены точки здания, где напряжения достигали максимальных значений.
|
σ11 |
σ22 |
|
Рисунок 2. Изолинии напряжения σ11 в безразмерном времени τ=52.35 |
Рисунок 3. Изолинии напряжения σ22 в безразмерном времени τ=38.30 |
σ12
Рисунок 4. Изолинии напряжения σ12 в безразмерном времени τ=52.58
Расчеты показали, что при поперечных колебаниях двухэтажных зданий максимальные значения нормальных напряжений ![]() и
и ![]() достигаются в центральной точке нижней части внешней несущей стены здания с координатами
достигаются в центральной точке нижней части внешней несущей стены здания с координатами ![]() Максимальные значения касательного напряжения
Максимальные значения касательного напряжения ![]() обнаружены в крайних точках нижней части внешней несущей стены с координатами
обнаружены в крайних точках нижней части внешней несущей стены с координатами ![]() .
.
На рис. 5–7 приведены графики изменения по безразмерному времени ![]() нормального и касательного напряжений
нормального и касательного напряжений ![]() ,
, ![]() и
и ![]() во внешней несущей стене двухэтажного здания. На рис. 5 приведен график изменения напряжения
во внешней несущей стене двухэтажного здания. На рис. 5 приведен график изменения напряжения ![]() по безразмерному времени
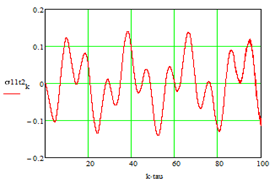
по безразмерному времени ![]() . Установлено максимальное значение напряжения, равное
. Установлено максимальное значение напряжения, равное ![]() (см. рис.5).
(см. рис.5).
На рис.6 приведен график изменения по безразмерному времени ![]() напряжения
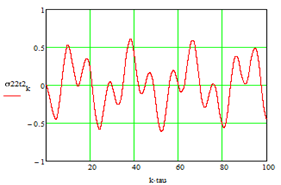
напряжения ![]() . Максимальное значение нормального напряжения
. Максимальное значение нормального напряжения ![]() в центральной точке нижней части внешней несущей стены здания получилось равным
в центральной точке нижней части внешней несущей стены здания получилось равным ![]() .
.
|
|
|
|
Рисунок 5. График напряжения |
Рисунок 6. График напряжения |
На рис. 7 приведен график изменения напряжения ![]() от безразмерного времени
от безразмерного времени ![]() . Как видно, максимальное значение касательного напряжения равно
. Как видно, максимальное значение касательного напряжения равно ![]() МПа (см. рис. 7).
МПа (см. рис. 7).

Рисунок 7. График напряжения ![]() по времени двухэтажного здания при поперечных колебаниях
по времени двухэтажного здания при поперечных колебаниях
На основе анализа численных результатов можно отметить, что максимальные значения перемещений достигаются на верхнем уровне, а максимальные значения напряжений – на нижнем уровне зданий. Преимуществом предлагаемой методики динамического расчета зданий на основе пластинчатой континуальной модели является приведение трехмерной задачи к двухмерной, а также получение возможности вычисления высокой точности численных результатов для пластинчатого сооружения в виде пространственной модели многоэтажных зданий.