Колебания коробчатой конструкции крупнопанельных зданий при динамических воздействиях
Конференция: XXVII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Механика деформируемого твердого тела

XXVII Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Колебания коробчатой конструкции крупнопанельных зданий при динамических воздействиях
VIBRATIONS BOX CONSTRUCTION, LARGE-PANEL BUILDINGS UNDER DYNAMIC IMPACTS
Mahamatali Usarov
Doctor of science. Academy of Sciences of the Republic of Uzbekistan, Institute of Mechanics and seismic stability of structures named after M.T. Urazbaev, Uzbekistan, Tashkent
Giyosiddin Mamatisaev
Senior teacher Ferghana Polytechnic Institute, Uzbekistan, Ferghana
Аннотация. Статья посвящается усовершенствованию модели коробчатой конструкции зданий, учитывающей силы и моменты в зонах контактного взаимодействия балочных и пластинчатых элементов. Приведены уравнения движения элементов коробки, граничные условия на основании коробки и контактные условия между элементов коробки, а также, построена графиков перемещения панелей и балок.
Abstract. The paper is devoted to improvement of the model of box-like structure of the building, which accounts the forces and moments in the zones of contact interaction of beam and plate elements. An equation of motion of the elements of the box, boundary conditions in the base of the box and contact conditions between the elements of the box are given as well as drew graphs displacement of plates and beams.
Ключевые слова: Здания; коробчатая конструкция; динамический расчет; перемещение; напряжение; деформация; уравнение движения; граничные условия; контактные условия.
Keywords: buildings; box-like structure; dynamic design; displacement; stress; strain; equation of motion; boundary conditions; contact conditions.
В научных трудах М.М Мирсаидова [1-4] рассмотрены разные динамические задачи в плоской и пространственной постановке, посвященные оценки и прогнозирования динамического поведения грунтовых плотин различной высоты с учетом больших деформаций (геометрической нелинейности) и неоднородных особенностей конструкций при многокомпонентных кинематических воздействиях.
В работе [5] рассматриваются колебания элементов конструкции из изотропной вязкоупругой пластинки переменной толщины, находящиеся под действием равномерно распределённой вибрационной нагрузки, приложенной по одной из параллельных сторон, приводящей (при определённых сочетаниях частот собственных колебаний и возмущающей силы) к параметрическому резонансу.
В статьи [6,7] посвящены разработке методов динамического пространственного расчета конструкции на основе метода конечных разностей в рамках бимоментной теории, учитывающей пространственное напряженно-деформированное состояние. Были даны решения задачи о поперечных и продольных колебаниях зданий и сооружении с использованием пластинчатой модели, разработанной в рамках бимоментной теории пластин [8].
В теории колебаний тонкостенных элементов конструкций особое место занимают поперечные колебания консольных пластин и балок. Такие процессы описываются дифференциальными уравнениями высокого порядка. Поэтому удовлетворение граничным условиям, выбор координатных функций при применении вариационных методов или при аппроксимации конечно разностными формулами производных третьего и четвертого порядка является очень трудной задачей. Изучены свободные и вынужденные колебаний коробок крупнопанельного здания и ячеек каркасных зданий, а также в качестве расчетной схемы рассматривается пространственная коробка с защемленным нижним концом [11].
Целью работы является определение максимальных перемещений в панелях и стыковых соединениях элементов коробки с учетом оконных проемов.
Рассматривается динамическая задача колебания коробки здания, основание которых совершает колебания по закону:
![]() , (1)
, (1)
где ![]() и
и ![]() – амплитуда, и частота вынужденных колебаний.
– амплитуда, и частота вынужденных колебаний.
Предлагается аналитико-численный метод решения задачи колебания коробки здания с учетом пространственных деформаций с полными контактными условиями в зонах стыковых соединений панелей и балочных элементов коробки здания.
Прогиб изгибаемых панелей представим в виде:
![]() , (2)
, (2)
а перемещения панелей, работающих на сдвиг, запишем в виде:
![]() ,
, ![]() . (3)
. (3)
где ![]() – основная частота вынужденных колебаний.
– основная частота вынужденных колебаний.
Прогиб и угол закручивания балок представим в виде:
![]() ,
, ![]() (4)
(4)
где ![]() – основная частота внешнего воздействия,
– основная частота внешнего воздействия, ![]() - номер балок.
- номер балок.
Рассмотрим теоретический расчет коробки крупнопанельного здания при динамическом воздействии с учетом пространственной работы поперечных и продольных стен.
На основе представления (1) перепишем кинематические законы перемещения точек панелей. Нормальные перемещения точек изгибаемых панелей
![]() , (5,а)
, (5,а)
где ![]() - прогиб изгибаемых панелей,
- прогиб изгибаемых панелей, ![]() и
и ![]() –амплитуда и частота вынужденного колебания.
–амплитуда и частота вынужденного колебания.
Поле перемещения панелей, работающих на сдвиг, описывается функциями
![]() , (5,б)
, (5,б)
![]() . (5,в)
. (5,в)
Здесь ![]() - перемещения панелей, работающих на сдвиг.
- перемещения панелей, работающих на сдвиг.
В качестве уравнение движения изгибаемой панели принимаем [9,10] с учетом (1) запишется в виде
 (6)
(6)
где D – цилиндрическая жесткость панелей при поперечном изгибе.
 ,
, ![]() -толщина балки,
-толщина балки, ![]() - прогиб панели (работающих на изгиб).
- прогиб панели (работающих на изгиб).
Двумерные уравнения движения панели, работающей на сдвиг принимаем [9,10] и запишутся в виде
![]() (6,а)
(6,а)
![]() (6,б)
(6,б)
где B - цилиндрическая жесткость панелей при растяжении и сжатии.
![]() ,
,![]() - перемещения по осям ОХ и ОУ.
- перемещения по осям ОХ и ОУ.
Граничные условия на основании здания (![]() ) запишем как для жесткого защемления. Нижняя часть здания перемещается вместе с основанием
) запишем как для жесткого защемления. Нижняя часть здания перемещается вместе с основанием
![]() ,
, ![]() ; (7)
; (7)
При этом поворот отсутствует
![]() . (8)
. (8)
Граничные условия (7) и (8) при х=0 с учетом (5) перепишутся виде:
![]() ,
,![]() , (9,а)
, (9,а)
![]() ,
, ![]() . (9,б)
. (9,б)
Граничные условия на верхнем конце![]() имеют вид:
имеют вид:
Контактные условия на стыках перекрытия и стены, работающей на изгиб, запишутся в виде
 (10,а)
(10,а)
Контактные условия на стыках перекрытия и стены, работающей на сдвиг, относительно контактного касательного напряжения, запишутся в виде
![]() . (10,б)
. (10,б)
Контактные условия на стыках перекрытия и стены, работающей на сдвиг, относительно контактного нормального напряжения, запишутся в виде
![]() . (10,в)
. (10,в)
В качестве исходных данных задаются следующие параметры:
отношение высоты к ширине изгибаемой панели![]() , отношение высоты к ширине панели, работающей на сдвиг
, отношение высоты к ширине панели, работающей на сдвиг![]() . Отношение толщины к ширине изгибаемой панели
. Отношение толщины к ширине изгибаемой панели![]() , а отношение толщины изгибаемой панели к толщину панели, работающей на сдвиг
, а отношение толщины изгибаемой панели к толщину панели, работающей на сдвиг![]() .
.
Отношение модулей упругости, изгибаемой панелей и панели, работающей на сдвиг![]() . Коэффициент Пуассона материалов панелей равен
. Коэффициент Пуассона материалов панелей равен![]() .
.
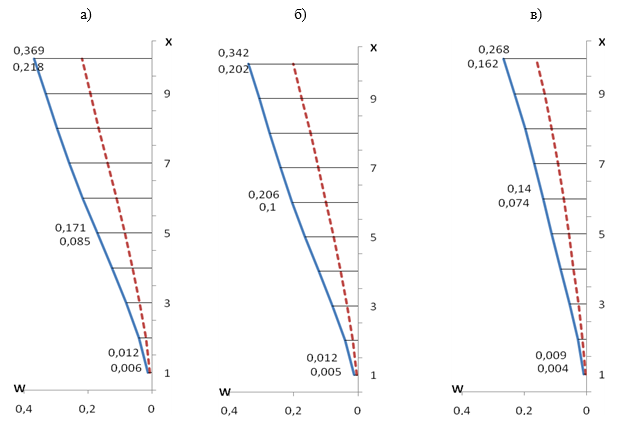
Рисунок 1. Изменения прогибов панелей, работающих на изгиб
а) середины, б) края проема, в) края панели
На рис1. приведены графики, характеризующие изменения по вертикали безразмерного максимального прогиба![]() , на трех характерных сечениях панелей, работающих на изгиб, от середины панели к одному из ее краев. Как видно, прогибы панелей увеличиваются с приближением к середине панелей.
, на трех характерных сечениях панелей, работающих на изгиб, от середины панели к одному из ее краев. Как видно, прогибы панелей увеличиваются с приближением к середине панелей.
Максимальное значения прогиба (рис1.а), которое достигается на верхней точке вертикального сечения, расположенного в середине, изгибаемой панелей равно
![]()
Максимальное значение полного горизонтального смещения верхней точки изгибаемой панели определяется по формуле (5,а) и равно
![]()
Как и следовало ожидать, максимальные значения перемещения обнаружены на верхних точках панелей и балок.
На рис.2. показаны графики изменения по вертикали безразмерного максимального прогиба![]() балок.
балок.
Расчеты показывают, что (рис.2.) балок, которые расположены на стороне действии нагрузки, изгибаются больше чем балок, которые расположены против о стороне действии нагрузки.
Максимальное значения прогиба (рис 2.а), которое достигается на верхней, точке, изгибаемой балок:
![]()
Тогда максимальное значение полного горизонтального смещения верхней точки изгибаемой панели определяется по формуле (5,а) и равно
![]()
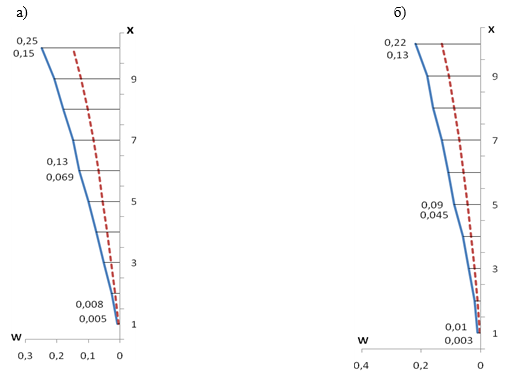
Рисунок. 2. Изменения прогиба по высоте балки
а) балка, на стороне действии нагрузки б) балка, против о стороне действии нагрузки
Из рис.2. видно, что прогиб вертикального края изгибаемой панели в несколько раз меньше прогиба средней части, так как края панели удерживаются поперечными панелями, которые работают на сдвиг, поэтому, формы изгиба балочных элементов и панелей не идентичные.
Как и следовало ожидать, максимальные значения перемещения обнаружены на верхних точках панелей и балок.
На рис 3. показаны графики изменения безразмерного перемещения и прогиба
и прогиба на панелях зависимости во времени.
на панелях зависимости во времени.
|
а) |
|
Рисунок. 3. График изменения безразмерного перемещения и прогиба: а) в панелей, работающие на сдвиг; б) в панелей, работающие на изгиб
Остальные численные результаты, характеризующие изменения во времени перемещения полученными с учетом начальных условий.
Заключения
1. Приведены уравнения движения точек панелей и балок коробки зданий, граничные, контактные и начальные условия задачи вынужденных колебания.
2. В рамках методах конечных разностей разработана методика динамического расчета перемещения в балочных и панельных элементах коробчатых конструкций зданий;
3. Графически представлены законы изменения максимальных значений прогибов и напряжений в характерных точках панелей и балочных элементов в зависимости от времени.



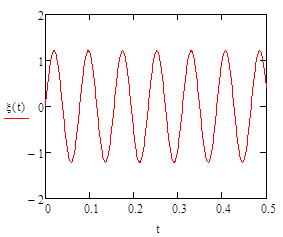 б)
б)