Пятиточечная разностная схема решения задач упругой устойчивости

FIVE-STAR DIFFERENCE SCHEME FOR SOLVING ELASTIC STABILITY PROBLEMS

Vahagn Petrosyan

Russian-Armenian university, Armenia, Yerevan

Harutyun Shmavonyan

Russian-Armenian university, Armenia, Yerevan

Аннотация. Рассматривается математическое моделирование колебаний изотропной прямоугольной пластинки в нестационарном магнитном поле. На основе теории тонких пластин получены основные уравнения и граничные условия, описывающие  динамическое поведение рассматриваемой магнитоупругой системы. Исходя из полученных уравнений сформулирована соответствующая задача математической физики которая решена численно и разработан алгоритм указанного численного метода.

Abstract. Considered mathematical modeling of the oscillations of an isotropic rectangular plate in a non-stationary magnetic field. Based on the theory of thin plates, the basic equations and boundary conditions are obtained that describe the dynamic behavior of the magnetoelastic system under consideration. Initially, from the obtained equations, the corresponding problem of mathematical physics was formulated.

Ключевые слова: изотропная пластинка; нестационарное магнитное поле; магнитоупругая система; численные методы.

Keywords: isotropic plate; non-stationary magnetic field; magnetoelastic system; numerical methods.

Введение.

Обшивка летательного аппарата — это внешняя оболочка, которая покрывает большую часть крыльев и фюзеляжа. Наиболее часто используемые материалы в обшивке – это материалы из алюминия и сплавов алюминия с другими металлами, в том числе цинка, магния и меди. От качества обшивки во многом зависят аэродинамика летательного аппарата.

В начале двадцатого века алюминий стал незаменимым материалом во самолётостроении. Блок цилиндров двигателя, который питал самолет Китии Хок братьев Райт был из цельной отливки, содержащей 8% меди. Алюминиевые лопасти для винтов появились еще в 1907 году, алюминиевые крышки, сиденья, капот, литые кронштейны и аналогичные детали быки распространены к началу Первой Мировой Войны.

В 1916 году Л. Брекет разработал разработал разведывательный бомбардировщик, который стал первым самолетом с использованием алюминия в рабочую структуру самолета. К концу войны, союзники и Германия, занялись алюминиевыми сплавами для структуры фюзеляжа и крыльев.

Обшивка не состоит из цельного куска сплавов, а из отдельных маленьких компонент, которые либо приклеены к корпусу летательного аппарата, либо прикручены с помощью винтов впотай. Эти различные компоненты соединены встык.

Однако, возникает серьезная проблема: как выбрать компоненты чтобы обеспечить максимальную живучесть самолета или же как вычислить максимально возможную скорость, которую вытерпит фюзеляж из выбранных компонентов. Колебания инженерных сооружений, отдельных компонентов летательных аппаратов, происходящие при взаимодействии с потоком газа, принято называть «флаттером».

Для решения данной задачи исследована сформулированная и известная в литературе математическая модель, которая является краевой задачей для дифференциального уравнения с частными производными.

Рассмотрим упругую изотропную прямоугольную пластинку постоянной толщины  отнесенную к декартовой системе координат  так, что срединная плоскость недеформированной пластинки совпадает с координатной плоскостью  . Пластинка занимает область  и находится под действием разного рода внешних воздействий (продольные механические нагружения, температурное поле, магнитное поле и т.д.). Тогда задача устойчивости рассматриваемой пластинки сводится к уравнениям [1]

                                                                                                           (1)

где  цилиндрическая жесткость,  неизвестных параметр характеризующий внешнее воздействие. Для ясности и наглядности будем ограничиваться случаем, когда два края пластинки шарнирно оперты а остальные два - жестко защемлены. Тогда решение поставленной краевой задачи будем искать в следующем виде [1]:

.                                                                                           (2)

Подставляя (2) в (1) получим следующее обыкновенное дифференциальное уравнение относительно неизвестных функции :

.                                                                               (3)

Представим уравнение (3) и граничные условия в конечных разностях [2]. Для этого на отрезке  построим сетку 

В общем случае стационарные конечно-разностные уравнения практически всегда являются аппроксимирующими для соответствующих дифференциальных уравнений, причем установить это довольно несложно. Представляя производные искомых функций и граничные условия в конечных разностях и подставляя в уравнение (3) получим следущую систему:

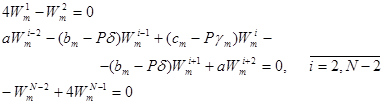                                                                         (4)

где введены следующие обозначения:

Системы вида (4) возникают при пятиточечной аппроксимации краевых задач для однородных обыкновенных дифференциальных уравнений четвертой степени с постоянными и переменными коэффициентами, а также при реализации разностных схем для уравнений в частных производных.

В последнем случае обычно требуется решить не единичную задачу, а серию задач, причем число задач в серии мижет равняться нескольким десяткам. Поэтому необходимо разработать экономичные методы решения задач вида (4) с малым числом действий. В настоящей работе приведен один из таких методов.

Итак, задача вычисления критического значения параметра  уравнения (4) сведена к вычислению минимального собственного значения обобщенной задачи собственных значений (4), т.е. нужно вычислить минимальный корень характеристического уравнения

                                                                                                       (5)

где

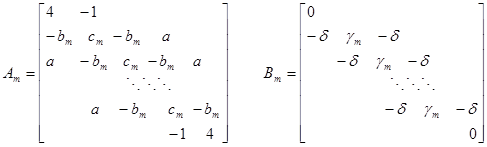.                                                                        (6)

Известно, что если степень характеристического уравнения меньше размерности матрицы, (т.е. у  есть нулевая строка и столбец), то обобщенная задача собственных значений имеет собственные значения стремящееся к бесконечности.

Как видно из (6), приведенный случай соответствует вышесказанному, следовательно наша задача имеет собственный корень стремящееся к бесконечности.

Часто бывает более удобным рассматривать матрицу (вектор) как построенной из матриц (векторов) маньших размерностей.

С учетом (6), можем представить

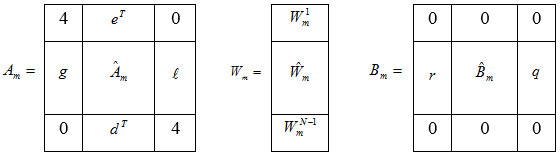
где

Следовательно, получим следующую задачу:

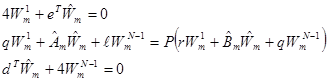                                                                                     (7)

или

                                                                                (8)

Тогда, характеристическое уравнение (5) примет вид

,                                                                                                       (9)

где

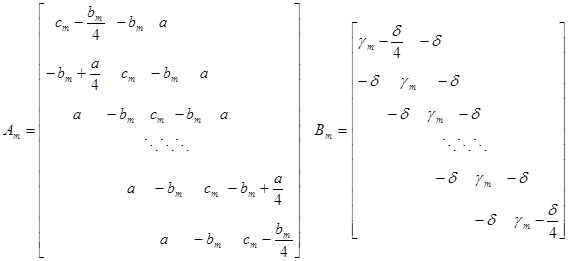
Легко доказать, что матрица  положительно определена (согласно критерии Сильвестра), следовательно, можно применить разложение Холеского [2].

Итак, задача устойчивости рассматриваемых пластин сведена к вычислению минимального собственного знчения обобщенной задачи собственных значений

                                                                                                            (10)

где . Применяя разложение Холеского  , где  – нижняя треугольная матрица,  – правая треугольная матрица и обозначения  получим

.                                                                                                             (11)

Наша цель вычислить минимальное собственное значение задачи (11), которую можно найти используя степенной метод [2]. Для этого перепишем (11) в виде

.                                                                                                   (12)

При произвольном начальном векторе  вычислим  последовательные приближения. Следовательно, согласно степенному методу,

.                                                                                                (13)

Итак, вычисляя  указанным методом, легко получить  минимальное собственное значение задачи (11). Проведен численный анализ для конкретной пластинки. Вычислена критическая нагрузка аналитическим методом  и предложенным численным методом , N=20.