Диагностики полимерных композиционных материалов применяемых в авиационных конструкциях

Аннотация. В статье рассматривается использование радиоволнового метода диагностики полимерных композитов авиационного назначения. Приведено описание процесса измерения и методом интегральных уравнений.

Ключевые слова: Полимерные композиционные материалы; углепластики; диэлектрическая проницаемость

Используемые обозначения и термины:

НКМ - низкоимпедансные композиционные материалы,

НК - разрушающий контроль,

МИУ - метода интегральных уравнений,

Введение

С 90 гг. прошлого века создаются новые полимерные композиционные материалы. Для отслеживания их свойств как в процессе изготовления и контроля готовых изделий авиационного назначения применяется не разрушающий контроль (НК). Наиболее информационным методом НК, является радиоволновые методы, в которых информационным параметром будет коэффициент отражения или коэффициент прохождения электромагнитной волны, в зависимости от структуры полимерного материала.

Произведем измерение e НКМ углепластика марки У-ПУ (название условное) волноводным методом по методике и измерительной схеме, для традиционных материалов изложенной в [1]. Образец измеряемого материала устанавливается на открытый конец волновода в качестве короткозамыкателя и по измеренному комплексному коэффициенту отражения вычислить значения e и tgd по формулам Френеля, для метода бесконечного слоя. Коэффициент отражения имеет вид  

,

где R – комплексный коэффициент отражения, e=e(1–j tgd), из формулы выражаются значения e и tgd :

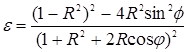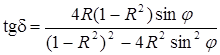,                  .                                                                    (1)

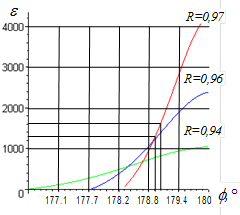
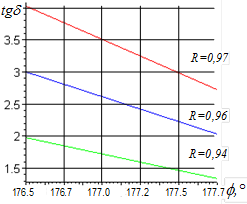
По формулам (1) построены зависимости относительной диэлектрической проницаемости e и тангенса угла диэлектрических потерь tgd от (|R|,j).

а                                                                       б

Рисунок. 1. Зависимости e и tgd от модуля |R| и фазы j коэффициента отражения

Из рис. 1 видно, что фаза коэффициента отражения j®180° графики очень быстро возрастают, имеют почти вертикальную зависимость, при небольшой инструментальной ошибки измерения фазы j получатся большая ошибка определения относительной диэлектрической проницаемости e, по данной методике.

Для повышения точности обработки получаемых результатов измерений характеристик изделия по его диэлектрическим параметрам, применяется более строгий с электродинамической точки зрения математический метод, метода интегральных уравнений (МИУ). Процедура составления интегральных уравнений производиться через поверхностные токи, наводимые на поверхности образца НКМ и металлической конструкции волноводного датчика зондирующей электромагнитной волной, подробна описана [2,3].

Модель электрически тонкого тела. Структура измерительного датчика на базе круглого волновода, МИУ позволяет численно рассчитать комплексный коэффициент отражения для рупора произвольной образующей [4]. Такая конструкция волноводного датчика эквивалентна схеме измерения в свободном пространстве. По аналогии с измерениями в свободном пространстве можно производить измерения диэлектрических параметров электрически тонких образцов НКМ (проводящие углепластики толщиной 1-2 мм, или стеклопластики используемые в качестве защитных колпаков, на радиолокатор самолета) на прохождение, добавив на выходе измерительного датчика приемную антенну (рис.2,б) или же эквивалент ее на круглом волноводе без рупора (рис.2,а).

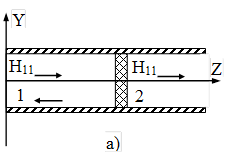
Рисунок.2. Конструкция волноводного датчика для измерений на прохождение:
а) – на круглом волноводе; б) – на круглом волноводе с коническим рупором.

Для измерения диэлектрических характеристик НКМ на прохождение электромагнитной волны сквозь материал, используется мощность повышенного уровня, которая на выходе образца измеряемого материала имеет достаточный уровень мощности для измерительных приборов. Причина повышения мощности измерения связана из-за большого затухания электромагнитной волны в НКМ. Такие измерения производятся на образцах НКМ малой толщины (порядка 0,5–2 мм).

В измерениях на прохождение электромагнитной волны измеряемый образец НКМ представляется как электрически тонкое тело. Измеряемым параметром являться комплексный коэффициент прохождения [3]. Составляется система интегральных уравнений для внешней (освещенной) и тыльной (теневой) границ тонкого тела, используя уравнения. На внешней поверхности (L1) поле зондирующей волны создается током , на тыльной поверхности (L2), прошедшая волна будет описываться наведенными токами  и . Процесс составления интегральных уравнений такой же, как и в [1], учитывая на границах L1 и L2 граничные условия [n,E]=Z[n,[n,H]], где n – внешняя нормаль, направленная в глубь образца НКМ, Z – диагональная матрица поверхностного импеданса . Матричный характер импеданса показывает, что он может быть различным по разным направлениям, при наличии анизотропии НКМ. Для импедансного тела. Запишем систему уравнений:

                                                                      (2)

                                                               (3)

                                                                 (4)

где p₁, q₁ точки на границе L1, а p₂ q₂ на границе L2

Уравнение (2) для внешней поверхности L1 аналогично уравнениям для однородного полубесконечного тела. Последний интегральный член в левой части его учитывает отражение от тыльной поверхности. Уравнения (3), (4) описывают поле прошедшей волны, при этом первые интегральные члены учитывают влияние внешней поверхности. На обоих поверхностях выполняются граничные условия , . Полученные уравнения представляют собой уравнения Фредгольма второго рода, которые решаются численными методами. Описываемый ток, в интегральных уравнениях на освещенной поверхности представляется как , на затененной поверхности .

Решение интегральных уравнений производится проекционный численный метод (метод Галеркина) [2].

По предложенной теории был проведен контроль образца НКМ. По результатам измерений было определено значение относительной диэлектрической проницаемости материала У-ПУ e=940±30% и тангенса угла диэлектрических потерь tgd=1,3±40%, имеющих модуль коэффициента отражения 0,94.