Автоматизация подбора оптимальных параметров для уравнения логистической кривой

Automating the selection of optimal parameters for the equation of the logistic curve

Rodion Kalyuzhin

student, Tomsk State University of Control Systems and Radioelectronics, Russia, Tomsk

Vladimir Korobko

graduate student, Tomsk State University of Control Systems and Radioelectronics, Russia, Tomsk

Natalya Zarikovskaya

Candidate of Physical and Mathematical Sciences, Associate Professor, Tomsk State University of Control Systems and Radioelectronics, Russia, Tomsk

Аннотация. Реализация приложения, позволяющего проводить анализ зависимости периода макролокализации пластической деформации от размера зерна для образцов поликристаллического материала, имеющей вид логистической кривой. Были использованы метод Хука-Дживса и метод градиентного спуска с постоянным шагом. Результаты работы приложения протестированы на реальных данных и хорошо согласуются с опубликованными ранее данными.

 Abstract. Realization of the application allowing to analyze the dependence of the period of macrolocalization of plastic deformation on grain size for samples of polycrystalline material having the form of a logistic curve. The Hook-Jeeves method and the gradient descent method with a constant step were used. The results of the application are tested on real data and are in good agreement with the previously published data.

Ключевые слова: математическая модель; пластическая деформация; механические свойства; размер зерна; Хук-Дживс; алгоритм.

Keywords: mathematical model; plastic deformation; mechanical properties; grain size; Hooke-Jeeves, algorithm.

В ходе многочисленных экспериментов для образцов поликристаллического алюминия марки A85 была получена зависимость периода макролокализации пластической деформации от размера зерна поликристаллического материала. Эмпирическим путем было установлено, что зависимость λ(d) на всем интервале размеров зерен описывается уравнением логистической кривой, имеющей вид (1)

                                                                                                (1)

которое является решением дифференциального уравнения Вольтера (2):

                                                                                                      (2)

где ,  С – безразмерная постоянная интегрирования, a и b  – положительные размерные константы.

Данная зависимость была получена для образцов поликристаллического алюминия A85, с следующими параметрами длина рабочей поверхность 50 мм, ширина рабочей поверхности 2 мм, толщина рабочей поверхности 2 мм. Предположительно данная зависимость должна проявляться для всех материалов и с различной геометрией рабочей поверхности.

Исходя из вышесказанного, предполагается что определение количественных характеристик по параметрам логистической кривой и уравнению Вольтера позволит более точно сформулировать математическую модель, описывающую зависимость параметров макролокализации пластической деформации от размеров зерна.

В ходе работы был проведен обзор существующих методов обработки экспериментальных данных.

Для реализации программного средства для подбора оптимальных параметров при получении аналитического решения был использован язык программирования C# и технология Windows Forms.

В ходе проведения обзора существующих методов, были выделены наиболее часто используемые методы:

- метод наименьших квадратов;

- интерполяция Лагранжа;

- кубический сплайн;

- сплайн Акимы;

- метод Хука-Дживса;

- метод градиентного спуска с постоянным шагом.

Наиболее качественные результаты, согласующиеся с экспериментальными данными, показали метод Хука-Дживса и метод градиентного спуска с постоянным шагом. Рассмотрим более подробно данные методы и их реализацию.

Поиск решения состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха идет поиск по образцу.

Сначала необходимо выбрать базисную точку (b₁) и шаг (h_j) для каждой переменной x_j. Далее вычисляется f(x) в b₁ с целью получения сведений о локальном поведении целевой функции. Функция f(x) в базисной точке находится следующим образом:

-  вычисляется значение точки f(b1);

-  каждая переменная по очереди изменяется прибавлением шага длинны.

Таким образом, мы вычисляем f(b₁+h₁e₁), где e₁ – единичный вектор в направлении оси x₁. Если это приводит к уменьшению значения функции, то базисная точка заменяется на b₁+h₁e₁, в противном случае вычисляется значение функции f(b₁ - h₁e₁), если ее значение уменьшилось, то b₁ заменяется на b₁ - h₁e₁. Если ни один из шагов не приводит к уменьшению значения функции, то базисная точка остается неизменной и рассматриваются изменения в направление оси x₂, то есть находится значение функции f(b₁ + h₂e₂) и так далее. Когда будут рассмотрены все n переменных, на выходе будет получена новая базисная точка b₂. Если уменьшение функции не было достигнуто (b₂ = b₁), то исследование повторяется вокруг той же базисной точки b₁, но с уменьшенной длинной шага, в противном случае производится поиск по образцу [1].

При выполнении поиска по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом [1]. Так как поиск в направлении b₂–b₁, уже привел к уменьшению значения функции, то вычислим функцию (3) в точке образца:

                                                                                                    (3)

Затем исследование продолжается вокруг точки P_j, если наименьшее значение на данном шаге меньше значений в базисной точке b_j+1, то получаем новую базисную точку b₃ = (b_j+2), в противном случае не производится поиск по образцу, а продолжается исследование в точке b₂ = (b_j+1). На рисунке 1 представлен результат многомерной оптимизации для двух различных целевых функций.

Рисунок 1. Результат применения метода Хука-Дживса для двух целевых функций

Вычислительный процесс завершается, когда длина шага будет уменьшена до заданного малого значения. В качестве альтернативного метода был рассмотрен метод градиентного спуска с постоянным шагом.

Основная идея метода состоит в оптимизации в направлении наискорейшего спуска, данное направление задается антиградиентом Ñf:

                                                                                        (4)

где     выбирается:

-     постоянной, в таком случае метод может расходиться;

-     дробным шагом;

-     наискорейшим спуском формула (5).

                                                                                   (5)

Метод прекращает свою работу, если достиг точки остановки (6) или (7):

                                                                                              (6)

                                                                                     (7)

где x^[k] Î Rⁿ – значение поученное после k-ого шага оптимизации;

 – заранее определенная точность.

Сходимость градиентного спуска с постоянным шагом доказывается теоремой: пусть функция f, дифференцируема, сильновыпукла константой . Пусть выполняется условие Липшица для градиента (8) [2].

                                                                                        (8)

Пусть 0 < l< 2/L, тогда:

                                                                            (9)

                                                                                       (10)

где    q – константа, характеризующая скорость сходимости метода, зависящая от шага .

На рисунке 2 представлен результат многомерной оптимизации методом градиентного спуска для двух различных целевых функций.

Рисунок 2. Результат применения метода градиентного спуска с постоянным шагом для двух целевых функций

Как видно из рисунка 1 и рисунка 2 метод градиентного спуска с постоянным шагом сходится быстрее, а также результат многомерной оптимизации является более точным.

Реализованный проект состоит из следующих пространств имен, разделенных для удобства разработки и дальнейшего сопровождения приложения на:

-  Components;

-  Data Transfer Objects (далее DTO);

-  Engine;

-  Services;

-  Settings;

-  Utils.

На рисунке 3 представлена зависимость пространств имён в данной реализации приложения.

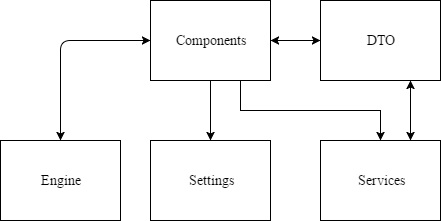
Рисунок 3. Диаграмма зависимостей пространств имён

Где пространство имен Components содержит все компоненты приложения. Каждая компонента имеет свое пространство имен, если состоит больше чем из одного класса. В пространстве имен компоненты содержатся все разработанные для нее элементы управления, а также классы, используемые только в данной компоненте.

DTO – один из шаблонов проектирования, используется для передачи данных между подсистемами приложения. Содержит все объекты, используемые для передачи данных. Данные объекты должны содержать только поля и свойства. Объекты DTO в данной реализации приложения используются для отделения данных от их обработки и предназначены только для загрузки и выгрузки данных, а также как источник данных для различных классов приложения.

Engine – данное пространство имен содержит служебные классы и интерфейсы, необходимые для работы системы модулей, а так же обслуживающие структурные элементы не относящиеся к обработке данных.

Services – содержит в себе сервисы, обслуживающие интерфейсы и реализации сервисов, предназначенные для передачи, загрузки и сохранения данных.

Settings – данной пространство имен состоит из классов настроек и служебных классов для работы с настройками приложения и модулей.

Utils – содержит классы с методами расширения [3] а так же реализации методов обработки данных.

Основным модулем приложения является анализатор кривых.

Модуль анализа кривых реализуется классом CurvesAnalisysComponent предназначен для построения кривых зависящих от набора изменяемых пользователем коэффициентов. Кривые отображаются на графике внутри компоненты, вместе с заданным набором точек, загружаемым из источника данных. Точки считаются реальными данными, а кривые построенной моделью. Точность модели определяется по критерию R², который является коэффициентом детерминации и рассчитывается по формуле (11):

                                                                                                    (11)

Количество кривых может быть произвольным, что представлено на рисунке 4, так же присутствует возможность не отображать кривую на общем графике.

Рисунок 4. Пример построения кривых на графике

При варьировании коэффициентов, кривая изменяется в реальном времени, также пересчитывается коэффициент детерминации. На рисунке 5 представлена форма добавления или редактирования кривой.

Рисунок 5. Форма добавления или редактирования кривой

В качестве дополнительной возможности предусмотрена максимизация коэффициента R² для построенной кривой и заданного набора точек с помощью метода градиентного спуска с постоянным шагом.

Предусмотрена возможность сохранения данных кривых, а также выгрузки данных по текущей кривой в формате имя кривой (зависимый параметр), уравнение кривой, варьируемые коэффициенты и их значения, коэффициент детерминации и его значение.

Присутствует возможность задавать диапазон по оси абсцисс. Данный диапазон применяется для кривой, экспериментальные точки игнорируются, что проиллюстрировано на рисунке 6.

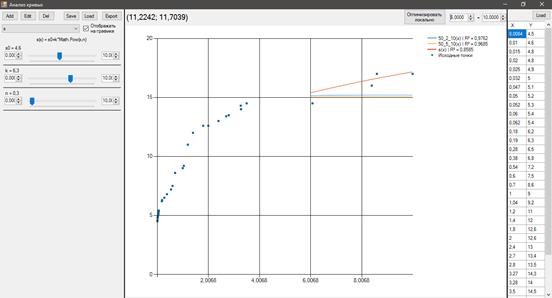
Рисунок 6. Пример применения диапазона к кривым

Компонента содержит три основных элемента управления, разделенного двумя разделителями, позволяющими пользователю изменять размер элементов управления.

Элемент управления CurvesPanelCtrl реализует работу с исходными данными кривых. Данные кривых содержатся в типизированной коллекции Curves типа BindingList с элементами класса CurveViewModel, являющимся реализацией паттерна ViewModel и предоставляющего доступ к данным структуры CurveDto, содержащей информацию по кривым. CurveViewModel также позволяет получить доступ к самой структуре CurveDto, а также существует конструктор позволяющий сыоздать CurveViewModel из CurveDto. Свойство SelecterdCurve позволяет получить доступ к выбранной кривой. На рисунке 7 представлена структура хранения данных кривой.

Рисунок 7. Структура хранения данных кривой

CurveViewModel реализует интерфейс INotifyPropertyChanged позволяющий подписчикам события PropertyChanged отследить изменения в кривой. Коллекция BindingList генерирует событие ListChanged при добавлении и изменении элементов, а также при событии PropertyChanged для типов, реализующих INotifyPropertyChanged. Таким образом можно отследить все изменения коллекции кривых извне.

При нажатии на соответствующие кнопки, CurvesPanelCtrl генерирует события LoadClick, SaveClick, ExportClick. При установки нового списка кривых, вызывается метод RefreshView, который обновляет отображение элемента управления в соответствии с данными выделенной кривой, затем генерируется событие CurvesLoaded. Компонента CurvesAnalisysComponent, обрабатывает события LoadClick, SaveClick обращением к сервису, реализующему интерфейс ICurveAnalisysDataService, для загрузки и сохранения соответственно списка объектов CurveDto. Обработчик ExportClick выводит диалог экспорта данных выделенной кривой, преобразует формат экспорта и сохраняет по выбранному пользователем пути. Обработчик CurvesLoaded обновляет данные кривых на элементе управления отображающем графики кривых в соответствии с данными кривых в элементе CurvesPanelCtrl.

Элемент управления ChartViewCtrl отображает динамично изменяющиеся графики кривых, а также экспериментальные точки. Для динамического отображения изменений кривых, ChartViewCtrl подписывается на событие ListChanged свойства Curves, и при вызове этого события соответствующим образом обновляет данные графиков. Так же ChartViewCtrl содержит кнопку оптимизации, при нажатии на которую генерируется событие OptimizeClick, которое обрабатывается компонентой. Обработчик этого события рассчитывает оптимальные значения коэффициентов, по методу градиентного спуска с постоянным шагом, до получения наилучшего значения R², а затем вызывает RefreshView у CurvesPanelCtrl, после чего данные графика обновляются.

Данные экспериментальных точек устанавливаются компонентой CurveAnalisysComponent. При изменении списка экспериментальных точек происходит обновление отображения на графике, а также пересчитываются значения коэффициента R² отображаемого в легендах кривых.

Данные для диапазона расчет значений кривых при загрузке компоненты получаются из настроек. При последующем изменении диапазона происходит изменение соответствующих настроек и их сохранение, после чего все кривые прорисовываются на заданном диапазоне значений. При перемещении мышки над графиком, в элементе управления Label отображаются координаты точки, в системе отсчета графика.

Загрузка и отображение данных экспериментальных точек происходит с помощью элемента управления ScatterPointsCtrl. Точки загружаются из файла, выбранного пользователем. Далее вызывается событие PointsChanged, которое обрабатывается компонентой CurvesAnalisysComponent, обработчик данного события устанавливает соответствующий набор экспериментальных точек в ChartViewControl.

Данные о периоде макролокализации пластической деформации для образцов поликристаллического алюминия марки A85 с геометрическими параметрами предоставлены лабораторией физики прочности НИУ ИФПМ СО РАН. Результаты, полученные с использованием разработанного приложения, хорошо согласуются с ранее опубликованными работами сотрудников лаборатории.

Полученные результаты будут использованы сотрудниками лаборатории для уточнения математической модели описывающих зависимость параметров макролокализации пластической деформации от основного структурного параметра поликристаллического материала – размера зерна.

Заключение

В настоящее время, на языке C#, было реализовано приложение позволяющие проводить анализ логистической кривой и осуществлять подбор основных параметров уравнения.