ПРЕОБРАЗОВАНИЕ ТАРЬЯНА-ВИШКИНА ДЛЯ НАХОЖДЕНИЯ ДВУСВЯЗНЫХ КОМПОНЕНТ ГРАФА

TARJAN-VISHKIN TRANSFORMATION FOR FINDING BICONNECTED COMPONENTS ОF GRAPH

Ivan Gordeev

Candidate of Sciences in Physics and Mathematics, associate professor in Astrakhan State University, Russia, Astrakhan

Aigul Nadtsyna

Student in Astrakhan State University, Russia, Astrakhan

Аннотация. В статье рассмотрено преобразование, используемое в алгоритме Тарьяна-Вишкина для нахождения двусвязных компонент графа. Преобразование заменяет исходный граф, двусвязные компоненты которого требуется найти, на новый граф, компоненты связности которого соответствуют двусвязным компонентам исходного.

Аbstract. The article considers the transformation used in the Tarjan-Vishkin algorithm for finding biconnected graph components. The transformation replaces the original graph biconnected components of which are to be found with a new graph connected components of which correspond to the biconnected components of the original one.

Ключевые слова: алгоритм Тарьяна-Вишкина; двусвязные компоненты графа.

Keyword: Tarjan-Vishkin algorithm; biconnected components of graph.

Введение. Для многих задач в научных исследованиях, где используются графовые модели, важным является нахождение двусвязных компонент в графе. Одним из наиболее эффективных и универсальных алгоритмов для нахождения двусвязных компонент является алгоритм, предложенный в 1985 году Робертом Тарьяном и Узи Вишкиным [2]. В данной статье рассматривается важный этап алгоритма Тарьяна-Вишкина: преобразование исходного графа в новый так, чтобы компоненты связности нового графа соответствовали двусвязным компонентам исходного графа. Статья Тарьяна и Вишкина [2] дает краткое формальное описание такого преобразования, однако, на наш взгляд, требуется более подробное пояснение данного преобразования. В некоторых источниках, предпринимающих попытку описать алгоритм Тарьяна-Вишкина на русском языке, о соответствующем преобразовании вообще не говорится [3].

Основная часть. В разных источниках даются разные, хотя и эквивалентные определения двусвязных компонент графа. В качестве синонима названия «двусвязная компонента» используется также термины компонента двусвязности или блок. [4, 5] Приведем два наиболее типичных определения двусвязных компонент:

Определение 1. Двусвязными компонентами графа называются классы эквивалентности рёбер, в которых два ребра принадлежат одному и тому же классу эквивалентности тогда и только тогда, когда они лежат на общем простом цикле. [4]

Определение 2. Блок (компонента двусвязности) графа − связный, непустой, не имеющий собственных точек сочленения максимальный подграф неориентированного графа. [5]

Точками сочленения называются вершины графа, при удалении которых увеличивается количество связных компонент графа. Точки сочленения принадлежат более, чем одному блоку. На Рис. 1 показан рассматриваемый далее в качестве примера граф  с 11 вершинами.

На Рис. 2 пунктиром обведены двусвязные компоненты (блоки) графа . Всего граф  имеет 6 двусвязных компонент.

Рисунок 1. Граф , рассматриваемый в качестве примера

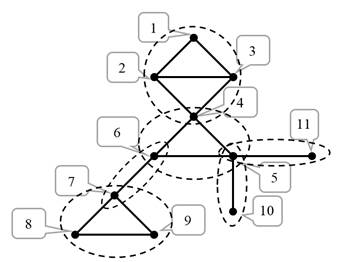
Рисунок 2. Обведенные пунктиром двусвязные компоненты графа 

На Рис. 3 подграфы, соответствующие блокам, изображены отдельно; при этом способе изображения точки сочленения дублируются в разных блоках. Точками сочленения являются вершины 4, 5, 6, 7.

Нахождение двусвязных компонент графа является актуальным для многих прикладных задач, в частности для нахождения остова перколяционного кластера.

В 1972 году Роберт Тарьян предложил рекурсивный алгоритм поиска в глубину, который может применяться для нахождения двусвязных компонент. [1]

Рекурсивный поиск в глубину не может быть распараллелен, поэтому в 1985 году Роберт Тарьян и Узи Вишкин предложили новый алгоритм для нахождения двусвязных компонент, использующий поиск в ширину и допускающий распараллеливание. [2]

Рисунок 3. Отдельное изображение блоков графа 

Рисунок 4. Граф , соответствующий графу 

Тарьян и Вишкин предложили правила для замены исходного графа  вспомогательным графом , так чтобы компоненты связности графа  соответствовали двусвязным компонентам графа . Вершины графа  – это ребра графа ; если  – множество ребер в графе , то  порождает двусвязную компоненту графа  тогда и только тогда, когда  порождает компоненту связности графа . Количество вершин в каждой компоненте связности графа  равно количеству рёбер в соответствующей двусвязной компоненте графа . На Рис. 4 показан граф , вершины которого соответствуют ребрам графа , а 6 компонент связности соответствуют 6 двусвязным компонентам графа , показанного на Рис. 1.

Вначале Тарьян и Вишкин предлагают выделить в графе  любое корневое остовное дерево . Оригинальный алгоритм Тарьяна использует для поиска двусвязных компонент только глубинное остовное дерево. Особенностью глубинного остовного дерева является то, что среди ребер , которые не вошли в дерево, есть только обратные ребра, соединяющие вершину с одним из ее предков, но нет поперечных ребер, которые соединяют две вершины не находящиеся в отношении предок-потомок. Однако для алгоритма Тарьяна-Вишкина не является существенным, чтобы дерево было древесным.

На Рис. 5 приводится пример возможного выбора дерева . Из 14 ребер графа  10 ребер выделено в качестве древесных (сплошные линии) и 4 ребра в качестве недревесных (пунктирные).

Рисунок 5. Ребра, выделенные в графе  как древесные (сплошные) и недревесные (пунктирные)

Пусть  – любое корневое остовное дерево графа , и пусть вершины  пронумерованы от  до  в порядке прямого обхода и каждую вершину идентифицируют по её номеру. Рёбра  обозначаются через , где  является родителем , обозначаемым .

Получаемое в результате преобразования граф  содержит каждое ребро графа  как вершину. Преобразование добавляет в граф  ребра трех видов.

Первый вид ребер графа : , где  является ребром , а  является ребром  таким, что . Здесь внутренние пары скобок ,  соответствуют рёбрам в исходном графе , которые являются вершинами в новом графе . Внешняя пара скобок  означает, что эти новые вершины соединены между собой в графе .

Неформально можно сказать, что ребра первого вида добавляются в граф , когда древесное ребро графа  смежно с недревесным ребром графа  и их общая вершина имеет номер больше, чем вершины на другом конце рёбер.

Рёбра графа  из примера, относящиеся к первому виду: ; ; ; . На Рис. 6 соответствующие ребра выделены красным цветом. Вершины графа , соответствующие древесным ребрам графа , показаны на Рис. 6 черными точками, а вершины, соответствующие недревесным ребрам, показаны серыми точками.

Рисунок 6. Три вида ребер в графе : красные – первый вид, желтые – второй вид, синие – третий вид

Второй вид ребер графа : , где  и  являются ребрами , а  является таким ребром , что  и  не имеют отношения предок-потомок в  (допускается ).

Неформально можно сказать, что ребра второго вида добавляются в граф , когда два древесных ребра графа , соединены поперечным недревесным ребром графа .

Рёбра графа  из примера, относящиеся ко второму виду:  (соединяющее недревесное ребро );  (соединяющее недревесное ребро );  (соединяющее недревесное ребро ). На Рис. 6 соответствующие ребра выделены желтым цветом.

Третий вид ребер графа : , где  и  являются ребрами , а некоторое ребро графа  соединяет потомка  с непотомком . Допускаются несобственные потомки.

Неформально можно сказать, что ребра третьего вида добавляются в граф , когда имеются два последовательных ребра дерева , для которых есть недревесное ребро графа  входящее с ними в простой цикл.

Рёбра графа  из примера, относящиеся к третьему виду: , вспомогательное ребро (потомок , непотомок )=; для рёбер , вспомогательное ребро ). На Рис. 6 соответствующие ребра выделены синим цветом.

Рисунок 7. Использование недревесных ребер в преобразовании: желтые – правило 2, синие – правило 3, зеленые – правила 2 и 3 одновременно

Заключение. Чтобы еще более подробно пояснить детали преобразования добавим еще Рис. 7, на котором помечено использование в преобразовании Тарьяна-Вишкина вспомогательных недревесных ребер. Желтым цветом на Рис. 7 помечены вспомогательные недревесные ребра графа , которые используются при добавлении в граф  ребер второго вида. Синим цветом на Рис. 7 помечены вспомогательные недревесные ребра графа , которые используются при добавлении в граф  ребер третьего вида. Зеленым цветом на Рис. 7 помечены вспомогательные недревесные ребра графа , которые используются при добавлении в граф  ребер и второго, и третьего видов.