ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМЫ САМОНАВЕДЕНИЯ РАКЕТ В БЛИЖНЕЙ ЗОНЕ И ПРИ ОБСТРЕЛЕ ВЫСОКОМАНЕВРЕННЫХ ЦЕЛЕЙ
Конференция: LI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Авиационная и ракетнокосмическая техника

LI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМЫ САМОНАВЕДЕНИЯ РАКЕТ В БЛИЖНЕЙ ЗОНЕ И ПРИ ОБСТРЕЛЕ ВЫСОКОМАНЕВРЕННЫХ ЦЕЛЕЙ
IMPROVING THE ACCURACY OF THE MISSILE HOMING SYSTEM IN THE NEAR ZONE AND WHEN FIRING AT HIGHLY MANEUVERABLE TARGETS
Do Quang Thong
Cand. of tech. sciences, lecturer (Le Quy Don Technical University) Hoang Quoc Viet, Vietnam, Hanoi
Аннотация. В настоящее время широко использована система самонаведения ракет (ССР) с применением метода пропорционального наведения. Исследования и практика применения показывают что это высокоточная система самонаведения. Однако результат моделирования показывает, что при обстреле целей, маневрирующих с большим нормальным ускорением при маленьком расстоянии между ракетой и целью ошибка наведения может составлять метры. ССР с такой ошибкой может не обеспечивать прямое попадание ракеты на цель. Поэтому в статье рассмотрена методика повышения точности ССР при обстреле высокоманевренных целей в ближней зоне. Оно достигается путём дополнительного ввода составляющей, пропорциональной ускорению угла наклона линии визирования ракеты и цели (ЛВРЦ) в закон наведения. Далее в статье предлагается методика синтеза ССР в среде Matlab. С целью упрощения процесса синтеза, в первом приближении принимаем линейную модель системы стабилизации нормального ускорения (ССНУ) и стараемся максимально использовать команды пакета Control System Toolbox (Matlab). Синтез ССНУ и ССР происходит одновременно. Выбор параметров ССНУ осуществляется при обеспечении её допустимого запаса устойчивости по амплитуде. Выбор параметров ССР осуществляется при обеспечении её минимальной ошибки наведения. При синтезе ССР предполагается что цель движется с постоянной скоростью и с постоянным нормальным ускорением. Такой подход позволяет синтезировать ССР с большой точностью.
Abstract. Currently, the missile homing system (MHS) is widely used using the proportional guidance method. Research and application practice show that this is a high-precision homing system. However, the simulation result shows that when firing at targets maneuvering with a large normal acceleration at a small distance between the missile and the target, the guidance error can be meters. The MHS with such an error may not provide a direct hit of the missile on the target. Therefore, the article considers a technique for improving the accuracy of the MHS when firing highly maneuverable targets in the near zone. It is achieved by additionally entering a component proportional to the acceleration of the angle of inclination of the line of sight of the missile and the target (LOS) into the law of guidance. Further in the article, the methodology of SSR synthesis in the Matlab environment is proposed. In order to simplify the synthesis process, we take a linear model of the normal acceleration stabilization system (NASS) as a first approximation and try to use the commands of the Control System Toolbox (Matlab) package as much as possible. The synthesis of MHS and NASS occurs simultaneously. The choice of NASS parameters is carried out while ensuring its permissible stability gain margin. The choice of MHS parameters is carried out while ensuring its minimum guidance error. In the synthesis of MHS, it is assumed that the target moves at a constant speed and with a constant normal acceleration. This approach makes it possible to synthesize MHS with great accuracy.
Ключевые слова: Синтез системы, ракета, система самонаведения ракет, метод пропорционального наведения.
Keywords: System synthesis, missile, missile homing system, proportional guidance method.
I. Введение
В настоящее время воздушные цели, особенно самолёты, произведённые по технологии стелс, имеют крайне малую эффективную поверхность рассеяния. Это приводит к значительному уменьшению дальности обнаружения радиолокационных станции. Поэтому в ССР с применением радиолокационных головок самонаведения достоверная информация о цели появляется только на крайне малой дальности до цели. Следовательно, переход на режим самонаведения ракеты только может начинаться на малой дальности до цели. Таким образом, ССР должна обеспечить необходимую точность на малой дальности. Кроме того, опытные лётчики часто выполняют резкий антиракетный манёвр при достижении малой дальности между ракетой и целью. Следовательно, ССР должна уничтожить цели, маневрирующие на малой дальности между ракетой и целью. При синтезе ССР с применением метода пропорционального наведения [1-4] предложено выбрать коэффициент пропорциональности kp в диапазоне 3-5. Однако, ССР с таким маленьким коэффициентом пропорциональности имеет большую ошибку наведения при обстреле высокоманёвренных целей [1]. С целью улучшения точности наведения на манёвренные цели в работе [1] предложен метод пропорционального наведения со смещением, и в работах [5, 6] предложены метод пропорционального наведения с упреждением и метод самонаведения по мгновенному промаху. Однако их техническая реализация сложная, требующая дополнительно определить ωa-проекцию угловой скорости линии визирования на антенную систему координат и ωц-составляющую, компенсирующую манёвр цели и.т.д.. Точное определение ωц на ракете сложно, требующее определение нормального ускорения цели [5, 6]. В ССР с применением метода пропорционального наведения с целью уничтожения целей на большом диапазоне высот применяют ССНУ. Устойчивость ССНУ является необходимым условием работы ССР [7]. При синтезе ССР необходимо синтезировать ССНУ. В работах [8] представлена методика синтеза ССР с допустимым запасом устойчивости ССНУ по амплитуде и по перерегулированию. Она позволяет получить высокоточную ССР. Однако, результат моделирования показывает, что при стрельбе цели, движущейся прямолинейно с постоянной скоростью 800 м/с. с начальной дальностью самонаведения меньше 6 км, ошибка наведения может достигать 2,6 м (Таб.1). В Таб.1 x0T-начальная горизонтальная дальность цели, y0T-начальная высота цели.
Таблица 1
Значения
|
x0T, м y0T, м |
5000 4000 |
5000 3500 |
5000 3000 |
5000 2500 |
5000 2000 |
5000 1500 |
5000 1000 |
5000 500 |
|
Ошибка наведения, м |
0,673 |
0,973 |
0,009 |
0,63 |
1,2 |
2,06 |
2,66 |
1,78 |
При стрельбе цели, маневрирующей на поздней стадии наведения ошибка наведения может достигать 3,1 м (Таб.2). В таб.2 цель имеет начальные координаты xT0=15000 м; yT0=5000 м; скорость 800 м/с; в момент t=4 с (5; 5,5 c; 5,8 c; 6 c; 6,3 c; 6,5 c; 7 с) после начала самонаведения цель начинает манёвр с ускорением -70 м/c2; время самонаведения составляет примерно 7,8 с.
Таблица 2
Значения
|
t, с |
4 |
5 |
5,5 |
5,8 |
6 |
6,3 |
6,5 |
7 |
|
Ошибка наведения, м |
0,021 |
0,07 |
0,23 |
1,062 |
1,79 |
1,96 |
1,4 |
3,1 |
Следовательно, ССР с такой ошибкой наведения может не обеспечить прямое попадание ракет на цель при обстреле цели на малой дальности или цели, маневрирующей на последней стадии самонаведения.
Таким образом, необходимо найти способ повышения точности ССР в ближней зоне действия и при стрельбе высокоманёвренной цели на последней стадии самонаведения.
II. Методика повышения точности системы самонаведения ракет в ближней зоне действия и при манёвре целей на последней стадии наведения
На практике широко применяют традиционный метод пропорционального наведения. Закон наведения метода имеет вид [1-6]:
![]()
где kp-коэффициент пропорциональности; φ угол наклона ЛВРЦ; ϴ-угол наклона вектора скорости ракеты.
Кинематическое исследование [9, 10] показывает, если коэффициент пропорциональности kp стремится к бесконечности, то метод пропорционального наведения превращается в метод параллельного сближения. Однако динамика элементов системы самонаведения препятствует выбрать коэффициент пропорциональности kp равно бесконечности. Для повышения точности наведения в [7] предлагается применить закон самонаведения:
![]()
где k-коэффициент; kp-коэффициент пропорциональности.
Результат моделирования показывает, что для уменьшения ошибки наведения целесообразно выбрать коэффициент пропорциональности kp в пределах 20-80. Тогда ошибка наведения возрастает при манёвре цели на последней стадии самонаведения (Таб.2). Поэтому предлагается дополнительно вводить в закон наведения составляющую, пропорциональную ускорению угла наклона ЛВРЦ. Тогда закон наведения имеет вид:
![]() (1)
(1)
где k1-коэффициент.
Для уменьшения влияния высокочастотных помех предлагается формировать сигнал, пропорциональный ускорению угла наклона ЛВРЦ реальным дифференциальным звеном с передаточной функцией (ПФ):
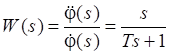
где T-постоянная времени.
Схема формирования сигнала скорость и сигнала ускорения угла наклона ЛВРЦ представлена на рис.1. На рис.1 Δx'0-разность координат между ракетой и целью на горизонтальной оси; Δy'0-разность координат между ракетой и целью на вертикальной оси; kgh- коэффициент преобразования прямой цепи головки самонаведения, k1- коэффициент преобразования прямой цепи реальной дифференциальной цепи (k2=1/T); φоб; φоб1-сигналы обратной связи; H-кинетический момент гироскопа.
III. Функциональная структура системы самонаведения ракет
Функциональная схема ССР с применением метода пропорционального
наведения в вертикальной плоскости представлена на рис.2 [7, 8].
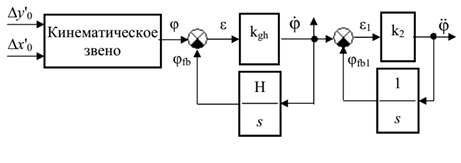
Рисунок 1. Упрощённая структурная схема ГСН и схема формирования сигнала ускорения ЛВРЦ
ССР с применением метода пропорционального наведения в вертикальной плоскости состоит из рулевого привода (РП), ракета, датчика угловой скорости (ДУС), датчика линейного ускорения (ДЛУ), гиростабилизованной головки самонаведения (ГСН), устройства расчёта скорости угла наклона траектории, формирователя закона стабилизации, формирователя закона наведения. На рис. 2: σs-закон стабилизации; σg-закон наведения; δ-угол вращения руля; ϑ угол тангажа; (Δy'0=y0T-y0)-разность высоты, (Δx'0=x0T-x0)-разность горизонтальной координаты между целью и ракетой.

Рисунок.2. Функциональна схема системы самонаведения ракет
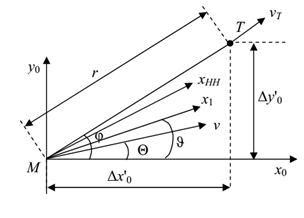
Рисунок 3. Взаимное положение ракеты и цели
Взаимное положение ракеты M и цели T представлено на рис.3. На рис.3 r-расстояние между ракетой и целей, xHH-направление оптической оси ГСН, x1- продольная ось ракеты, v- скорость ракеты, vT- скорость цели.
IV. Математические модели системы самонаведения ракет
В вертикальной плоскости математическая модель ракеты c закрепленными крылами в виде дифференциальных уравнений имеет вид [5, 7-13]:
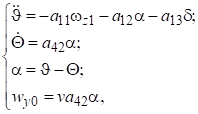 (2)
(2)
где α-угол атаки ракеты [градус]; ωz1-скорость вращения ракеты [градус/с]; a11-коэффициент естественного демпфирования [1/с]; a12-коэффициент флюгерности [1/с2]; a13-коэффициент эффективности руля [1/с2]; a42- коэффициент нормальной силы [1/с].
Из системы уравнений (2) можно получить математическую модель ракеты c закрепленными крылами в виде ПФ [8, 9, 10]:
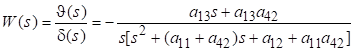 .
.
Математическая модель рулевого привода в виде передаточной функции (ПФ) имеет вид [8, 10, 12]:
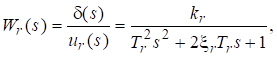
где kr [градус/В]-коэффициент преобразования; Tr [с]- постоянная времени; ξr- коэффициент демпфирования; ur-входной сигнал РП [В]. А в виде дифференциального уравнения (ДУ) она имеет вид:
![]() (3)
(3)
Математическая модель ДУС в виде ПФ имеет вид [10, 12]:

где kas [В/градус/с]-коэффициент преобразования; Tas [с]- постоянная времени; ξas- коэффициент демпфирования; uas,-выходной сигнал ДУС [В]. А в виде ДУ она имеет вид:
![]() . (4)
. (4)
Математическая модель ДЛУ в виде ПФ имеет вид [10, 12]:
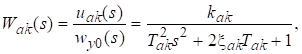
где kак [В/м/с2]-коэффициент преобразования; Tак [с]- постоянная времени; ξак- коэффициент демпфирования; uak,-выходной сигнал ДЛУ [В]. А в виде ДУ она имеет вид:
![]() . (5)
. (5)
Упрощённая схема гиростабилизованной ГСН представлена на рис.2 [8]. По рис. 2, (не нарушается общность при предположении H=1), математическая модель упрощённой гиростабилизованной ГСН имеет вид:
 (6)
(6)
и математическая модель схемы формирования ускорения угла ЛВРЦ имеет вид:
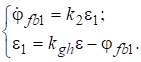 (7)
(7)
Закон стабилизации имеет вид [8]:
![]()
где kw, kωz1-коэффициенты.
Закон наведения (1) с учётом (1), (2), (6) и (7) имеет вид:
![]() . (8)
. (8)
Из (2)-(8) математическая модель ССР в виде системы ДУ первого порядка в вертикальной плоскости имеет вид:
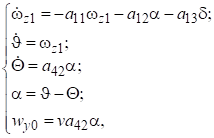 (9)
(9)
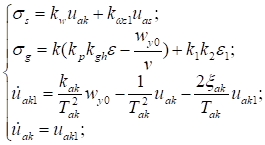 (10)
(10)
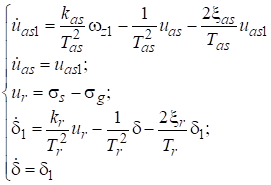 (11)
(11)
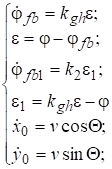 (12)
(12)
 (13)
(13)
 (14)
(14)
где x0 [м], y0 [м]-координаты ракеты по горизонтальной и вертикальной осям; x0T [м], y0T [м]-координаты цели по горизонтальной и вертикальной осям; ϴT-угол наклона траектории цели [градус]; wT-нормальное ускорение цели [м/с2]; T*-время наведения [с].
V. Синтез системы самонаведения ракет методом параметрической оптимизации
Задача синтеза ССР состоит в определении оптимальных значений коэффициентов (kωz1opt, kwopt, kopt, kpopt, k1opt), обеспечивающих найменьшую ошибку наведения. Мы осуществляем его методом параметрической оптимизации в среде Matlab. Здесь целевая функция-ошибка наведения f(kωz1, kw, k, kp, k1) не имеет явного выражения. Для её нахождения необходимо проинтегрировать системы уравнений (9-14) с начала до конца процесса самонаведения. Существуют различные методы синтеза ССР: синтез ССР с допустимым запасом устойчивости по амплитуде ССНУ; синтез ССР с допустимым перерегулированием ССНУ; синтез ССР с минимальным временем переходного процесса ССНУ; синтез ССР с минимальной ошибкой ССНУ... Рассмотрим методику синтеза ССР с допустимым запасом устойчивости по амплитуде ССНУ.
Математическая модель ССНУ ракеты при учёте динамики РП, ДУС, ДЛУ, инерционного звена в цепи главной обратной связи ССНУ в виде ПФ имеет вид
![]() (15)
(15)
Определим ПФ (15) с помощью команд пакета Control System Toolbox (Matlab) [8, 14]. Применить команду tf для описания ПФ динамического звена; применить операцию произведения (*) для определения ПФ последовательных соединённых динамических звеньев; применить команду feedback для определения ПФ замкнутого контура sysk.
С целью упрощения расчёта, в статье ошибка наведения определяется расстоянием между ракетой и целью в конце процесса самонаведения. Скорости ракеты и цели считаются постоянной. Пропускается ослепленность ГСН.

Рисунок 4. Алгоритм оптимизации системы самонаведения ракет
Мы должны обеспечить высокую точность при стрельбе цели в ближней зоне и при стрельбе высокоманевренной цели на последней стадии самонаведения. Поэтому задаётся малое начальное условие (маленькое начальное расстояние между ракетой и целей) и предполагается что цель маневрирует с постоянным нормальным ускорением.
Алгоритм параметрической оптимизации ССР на компьютере содержит такие основные шаги (рис.4).
Шаг 1: Ввод данных (рис.4).
Шаг 2: Предварительно синтезируем ССНУ (рис.4). Сканируем параметр kωz1 от значения kωz1min со “сравнительным большим” шагом сканирования dkωz1. Для каждого значения kωz1 сканируем параметр kw от значения kwmin со “сравнительным большим” шагом сканирования dkw. Для каждой пары коэффициентов (kωz1, kw) с помощью команд пакета Control System Toolbox [8, 14] опишем передаточную функцию открытой (sysh) и замкнутой системы ССНУ (sysk).
Далее, выберем только пары параметров (kωz1, kw) обеспечивающих устойчивость ССНУ по критерию Гурвица. Следовательно, надо определить коэффициенты передаточной функции замкнутой ССНУ командой [nm,dn]=tfdata(sysk,'v') [8, 14]. Из параметров полученного вектора dn (параметры характеристического многочлена) составим квадратные матрицы порядка 1-9. Определим значение определителей Гурвица командой det(x).
Если критерий устойчивости Гурвица выполнится, то определим значения запаса устойчивости по амплитуде командой [Gm,Pm,Wcg,Wcp]=margin(sysh) [14]. Если запас устойчивости ССНУ по амплитуде Gm находится в диапазоне 5-30 дБ, то перейдём на шаг 3.
Шаг 3: Сканируем параметр k от значения kmin со “сравнительным большим” шагом сканирования dk. Для каждого значения k сканируем параметр kp от значения kpmin со “сравнительным большим” шагом сканирования dkp. Для каждого значения kp сканируем параметр k1 от значения k1min со “сравнительным большим” шагом сканирования dk1. Для каждого набора параметров (kωz1, kw, k, kp, k1) проинтегрируем системы уравнений (9-14) с начала до конца процесса самонаведения для нахождения ошибки наведения r1. Если ошибка наведения r1 меньше 1 м (или некоторого значения), то перейдём на шаг 4.
Шаг 4: Присвоим a1=kωz1; a2=kw; a3=k; a4=kp; a5=k1. С полученным высше набором параметров (kωz1, kw, k, kp, k1) сканируем kωz1 от значения (a1-dkωz1) с шагом сканирования dkωz1/N1; kw от значения (a2-dkw) с шагом сканирования dkw/N2; k от значения (a3-dk) с шагом сканирования dk/N3; kp от значения (a4-dkp) с шагом сканирования dkp/N4; ; k1 от значения (a5-dk1) с шагом сканирования dk1/N5 (Ni≥5). С каждым набором параметров (kωz1, kw, k, kp, k1) проинтегрируем системы уравнений (9-14) с начала до конца процесса самонаведения для нахождения ошибки наведения r.
Сканирование параметров (kωz1, kw, k, kp, k1), интегрирование систем уравнений (9-14) и нахождение ошибки наведения r в шаге 4 повторяются до тех пор пока k1≤(a5+dk1); kp≤(a4+dkp); k≤(a3+dk); kw≤(a2+dkw); kωz1≤(a1+dkωz1).
Операции в шагах 2, 3, 4 повторяются до тех пор пока k1≤ k1max;kp≤ kpmax; k≤kmax; kw≤ kwmax; kωz1≤ kωz1max.
Шаг 5: Найдём набор оптимальных параметров (kωz1opt, kwopt, kopt, kpopt, k1opt) обеспечивающих наименьшую ошибку наведения rmin.
Предполагается [7] a11=1,2 1/с; a12=20 1/с2; a13=30 1/с2; a42=1,5 1/с; v=1300 м/с; kр=1 градус/В; ξр=0,6; Tр=0,05 с; δmax=±20 град; kг=1 В/градус/с, ξг=0,6; Tг=0,05 с; kак=1 В/м/с2, ξак=0,6; Tак=0,05 с; kgh=50; T1=0,3 с; k2=50; kωz1min=0,06; kωz1max=0,4; dkωz1=0,06; kwmin=0,001; kwmax=0,03; dkw=0,005; kmin=1; kmax=22; dk=5; kpmin=20; kpmax=60; dkp=5; k1min=1; k1max=40.
Предполагается x0T=5000 м, y0T=1500 м; vT=800 м/с; ϴT=180 град; wT=-70 м/с2.
После проведения параметрической оптимизации ССР по высше представленной методике в среде Matlab получили kωz1opt=0,15; kwopt =0,003; kopt=14; kpopt=16; k1opt=13. Ошибка наведения 0,004 м.
VI. Компьютерное исследование синтезированных ССР
Исследуем точность синтезированных ССР при стрельбе цели, движущейся прямолинейно с постоянной скоростью 800 м/с в ближней зоне. Ошибка наведения ракет при различных начальных координатах целей приведена в таб.3.
Таблица 3
Ошибка наведения ракет при различных начальных координатах целей
|
x0T, м y0T, м |
5000 4000 |
5000 3500 |
5000 3000 |
5000 2500 |
5000 2000 |
5000 1500 |
5000 1000 |
5000 500 |
|
Ошибка наведения, м |
0,27 |
0,76 |
1,08 |
0,326 |
0,123 |
1,08 |
1,35 |
0,77 |
Рассмотрим случай стрельбы высокоманёвренной цели на на последней стадии наведения. Предполагается, что цель имеет начальные координаты x0T=15000 м; y0T=5000 м; скорость 800 м/с; в момент t=4 с (5; 5,5 c; 5,8 c; 6 c; 6,3 c; 6,5 c; 7 c) после начала самонаведения цель начинает манёр с ускорением -70 м/c2; общее время самонаведения составляет примерно 7,8 с. Ошибка наведения ракет приведена в таб.4. Траектории ракеты и цели при t=5 c представлены на рис.5.
Таблица 4
Траектории ракеты и цели при t=5
|
t, с |
4 |
5 |
5,5 |
5,8 |
6 |
6,3 |
6,5 |
7 |
|
Ошибка наведения, м |
0,131 |
0,048 |
0,196 |
0,265 |
0,205 |
0,793 |
0,81 |
1,91 |
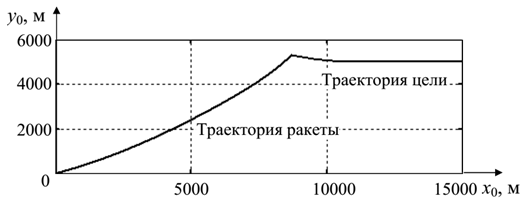
Рисунок 5. Траектории ракеты и цели
Из таб.1-таб.4 следует, что ССР с предложенным законом наведения незначительно точнее чем ССР с традиционным законом наведения при стрельбе целей в ближней зоне и высокоманёвренных целей.
Заключение
Предложенный закон наведения позволяет синтезировать высокоточную ССР. ССР с применением предложенного закона способна уничтожить цели маневренные с большим нормальным ускорением в ближней зоне с большой точностью. Предложенная методика синтеза ССР довольно проста, т.к. она в основном использует команды пакета Control System Toolbox для описания и синтеза ССНУ. Они позволяют выбрать параметры ССР с большой точностью наведения.


