МОДЕЛЬ ВАРИАЦИИ ДЕБИТОВ СКВАЖИН С ГОРИЗОНТАЛЬНОЙ ТРЕЩИНОЙ

MODEL OF VARIATION OF WELL FLOW RATES WITH HORIZONTAL FRACTURE

Tursinbay Turymbetov

Acting associate professor, Candidate of technical sciences, International University of Tourism and Hospitality, Kazakhstan, Turkestan

Разработка нефтяных и газовых месторождений с течением времени изменяет свои производительности, из-за влияния на работу скважин различных физико-химических и технологических факторов, которые проявляются, в основном в призабойной зоне продуктивных пластов. Эти факторы в основном снижают дебитов жидкости добывающих скважин [1], ухудшая, тем самым основные технологические процессы добычи углеводородной продукции. Поэтому для повышения дебита скважины применяется различные мероприятий, позволяющие увеличить гидродинамические параметры разрабатываемых пластов, в призабойной зоне коллектора. Одним из них является метод гидравлического разрыва пласта (ГРП). Благодаря ГРП в призабойной зоне скважины будет образовываться разные разносторонно-ориентированные своеобразные каналы, так называемые трещины. Среди известных трещин наиболее часто проявляются каналы в вертикальной и горизонтальной плоскостях, эффективность которых по-разному оценивается из-за влияния на состояние вновь созданных структурных изменений. Наиболее активно факторов способствующих изменить период интенсивной фильтрации флюидов в пласте по-разному способствует увеличению производительности добывающих скважин [2]. Если по некоторым скважинам ГРП способствует максимальному увеличению их дебитов, а по другим приводить к минимальному росту. По-видимому, это связано с тем, что темп фильтрации флюидов в призабойной зоне пласта (ПЗП) в основном зависит от размеров трещин и физико-химических свойств жидкостей, движущейся по искусственно созданным каналам, т.е. трещинам. Поэтому в настоящей работе рассматривается решение задачи позволяющее установить максимальный дебит скважины, при наличии в ПЗП горизонтальной трещины.

Рассматривается конечный пласт, круговой формы с непроницаемой кровлей и подошвой, в котором после гидравлического разрыва образовалась горизонтальная трещина с радиусом распространения R₀ и величиной раскрытия δ.

Для простоты считаем, что скважина находится в центре кругового пласта (см. рисунок. 1).

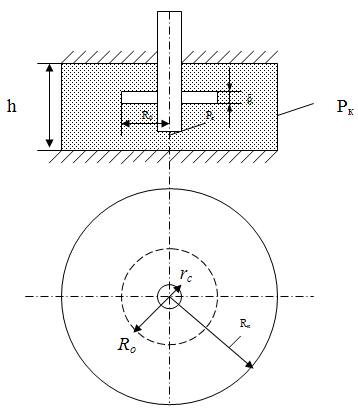
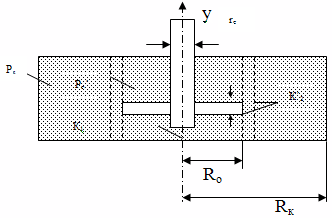
Рисунок 1. Схема нефтяного пласта с горизонтальной трещиной

Р_к и Р_с - соответственно давлений на контуре пласта и на забое скважины; R_к и r_с - соответственно радиус контура питания и скважины; R_о - радиус горизонтальной трещины.

Пласт считается однородным и изотропным с проницаемостью K₁. Эквивалентная проницаемость трещины  [3].

Если величина раскрытости трещины δ будет измеряться в мм, и она (трещина) будет свободна, т.е. в ней не будет песка, а также проницаемость определяется в дарси, то, как указано в работе [3], параметр ξ имеет следующее числовое значение .

Для определения максимального значения дебита скважины воспользуемся следующим соображением. Допустим, что круговой пласт эксплуатируется путем добывающей скважины, расположенной в его центре (см. рисунок 2а). Если из пласта вынуть часть грунта, т.е. заменить в некотором объеме пласта проницаемость К₁ на К₂´=∞ (см. рисунок 2б), то очевидно, такая замена, по-видимому, при сохранении постоянного перепада давления (∆Р=Р_к-Р_с) приведет только к увеличению дебита скважины или в крайнем случае оставит дебита без изменения.

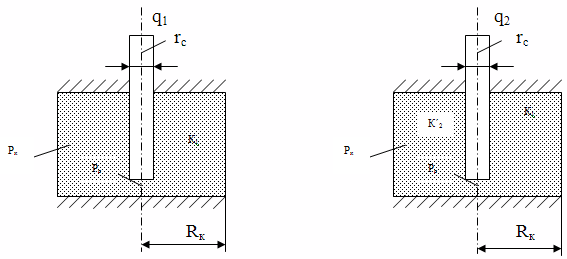
а)                         q₁ ≤ q₂                                     б)

Рисунок 2. Схема расположения скважины и некоторого вынутого объема грунта из кругового пласта

Учитывая это обстоятельство, сделаем мысленно на расстоянии R₀ от оси скважины кольцевой вырез на всю толщину пласта.

При этом предполагается, что вертикальная проницаемость кольцевого выреза равна бесконечности, т.е. К₂´ = ∞, и по толщине пласта в его пределах будет существовать некоторое постоянное давление равное Р₀´      (см. рисунок 3).

Рисунок 3. Схема расположения горизонтальной трещины и вертикального кольцевого выреза в круговом пласте

В работе [3] рассматриваемая задача решалась для однородного пласта, без учета упругости пласта и жидкости. Ниже нами предложены решение этой задачи с учетом указанных факторов.

Как видно из рисунка 3 в интервале  проницаемость пласта К₁. При этом предполагается, что в этой зоне будет происходить установившаяся фильтрация жидкости в пластической пористой среде [3]. Тогда в этом случае для определения величины притока к кольцевому вырезу можно воспользоваться формулой Горбунова А.Т. [4].

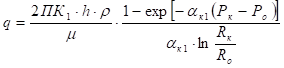                                                                                        (1)

От кольцевого выреза жидкость движется к скважине. Предполагается, что проницаемость в интервале  зависит от координаты y, а по радиусу r зависит от характера распределения давления Р_i(r) при изменении пластового давления. Поэтому для определения притока к скважине следует воспользоваться общей формулой полученной Горбуновым А.Т., в предположении, что существует пластическая пористая среда с трещиной в зоне пласта с сечениями r=r_c и r=R_o:   

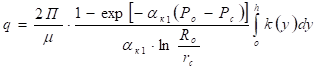                                                                                  (2)

где ρ и μ – плотность и вязкость жидкости;

α_к – коэффициент показывающий степень изменения гидропроводности пласта при изменении пластового давления на одну атмосферу или на 0,1 МПа;

к – проницаемость пласта, состоящая из трещины (к´₂) и пористого блока (к₁).

При этом величина К₁, в связи с изменением величины пластового давления будет меняться, из-за пластичности пористой среды, т.е. по следующей зависимости:

;                                                                                       (3)

где    К_1.0 - первоначальное значение проницаемости К₁ при начальном пластовом давлении Р_о.

Сама трещина эквивалентна слою с проницаемостью К₂.

Дебит этой же скважины до образования в пласте трещины определяется обычной формулой Дюпюи, с учетом пластичности пласта и упругости жидкости, полученной Горбуновым А.Т. [4].

Таким образом, общий дебит скважины из рассматриваемого пласта будет равен:

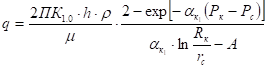;                                                                                            (4)

где

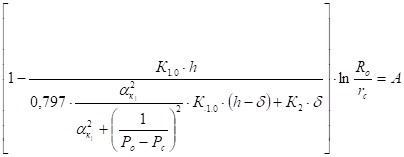
Если гидравлическому разрыву подвергалась несовершенная скважина с фильтрационным сопротивлением обусловленным несовершенством скважины как по степени так и по характеру вскрытия, т.е. С₁ +С₂ = С [3], то дебит до гидроразрыва определяется формулой:

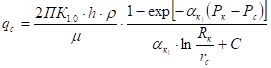;                                                                                        (5)

Дебит такой же скважины после гидравлического разрыва определяется по следующей формуле:

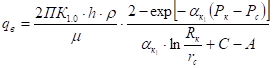                                                                                       (6)

где С–определяется по графикам Щурова [2], с учетом количества пулевых отверстий, глубины проникновения и их диаметра, а величина А–из формулы (4).

Таким образом, дебит найденный по формуле (4) или (6), является завышенным и в дальнейшем будет обозначаться q=q_в (верхняя граница).

Относительное увеличение дебита q_в по сравнению с q_c, т.е. эффект влияния трещины, выражается отношением

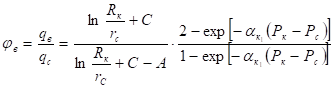;                                                                         (7)

Из соотношения (7) следует, что при образовании в пласте горизонтальной трещины параметр φ_в>1. С целью количественной оценки ниже приведены результаты расчетов по полученной формуле.

Для примера примем следующие исходные данные:

а) радиус контура питания              R_к = 1000 м.

б) радиус скважины                        r_c = 0,1 м.

в) коэффициент несовершенства скважины, как по степени, так и по характеру      с = 2,1

г) толщина пласта                           h₁ = 10 м.

д) проницаемость пласта                К_1.0 = 0,25 дарси = 0,25·10^-12 м2.

е) проницаемость трещины             К₂ = 83300 · δ².

ж) радиус трещины                         R_o = 25 м.

з) величина раскрытия трещины     δ = 1 мм.

и) давление на контуре питания     Р_к = Р_о = 25 МПа.

к) давление на забое скважины       Р_с = 18 МПа.

л) коэффициент изменения гидропроводности пласта .

м) величина давления                     Р_с´ = 21 МПа.

По формуле (4) определяем величину параметра А, которая равна:

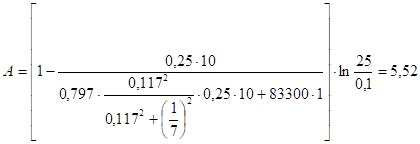
Затем по формуле (7) определяем максимальную величину относительного увеличения дебита скважины, которая равна:

.

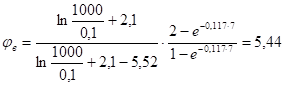Из полученных результатов видно, что величина максимального дебита скважины, при наличии в ПЗП горизонтальной трещины зависит достаточно от многих факторов, а именно: проницаемости порового пространства, трещины, ее размеров, изменения гидропроводности пласта, а также величин пластовых и забойных давлений.