Вычислимая имитационная модель анализа и оптимизации денежных потоков банковского отдела

COMPUTABLE SIMULATION MODEL FOR ANALYSIS AND OPTIMIZATION OF CASH FLOWS OF THE BANKING DEPARTMENT

Marina Belyaeva

candidate physical and mathematical sciences, associate professor, Sterlitamak Branch of Bashkir State University, Russia, Sterlitamak

Guzel Ayazgulova 

 student, Bashkir state University Sterlitamak branch, Russia, Sterlitamak

Аннотация. Разработка и реализация вычислимой имитационной модели анализа и оптимизации денежных потоков банковской системы на примере деятельности отделения коммерческого банка.

Abstract. the development and implementation of a computable simulation model for analysis and optimization of cash flows of the banking system on the example of the branch of the commercial Bank.

Ключевые слова: денежные потоки; имитационная модель; дискретно– событийная модель; система массового обслуживания; максимальная длина очереди; кредитный инспектор. 

Keywords: сash flows; simulation model; discrete - event model; queuing system; maximum queue length; credit inspector.

Одной из первостепенных задач, стоящих перед каждой банковской структурой, является ее постоянная адаптация к изменениям внешней среды, проявляющаяся в управлении кредитной и депозитной политиками, оптимизации филиальной сети и т.д.

Отделение коммерческого банка (ОКБ) является динамичной социотехнической системой, трансформирующейся с целью перехода в очередное устойчивое и управляемое состояние. Непрерывная оптимизация бизнес-процессов, обусловленная конкуренцией между банками и чувствительная к множеству случайных факторов, позволяет отнести ОКБ в разряд сложных, вероятностных и саморегулирующихся систем.

Сложность ОКБ как объекта моделирования приводит к тому, что процесс создания адекватной и пригодной к использованию имитационной модели становится многоуровневым, многоэтапным и циклическим, во многом определяется разветвленностью и иерархичностью организационной структуры банка, стохастичностью внешних возмущений. [1]

Структуру ОКБ можно рассматривать как систему двух взаимодополняющих подсистем– это операционный зал и отдел кредитования.

На рисунке 1 представлен общий процесс функционирования системы:

Рисунок 1. Процесс функционирования системы

КИ- Кредитный инспектор; ОФЛ-Отдел кредитования физических лиц; ОЮЛ- Отдел по работе с юридическими лицами; ОМБ – Отдел Малого Бизнеса. [2]

Результатом работы должно стать некоторое управленческое решение по оптимизации работы отделения Банка.

Основные параметры, характеризующие качество функционирования системы представлены в таблице 1.

Таблица 1.

Параметры функционирования системы

Имитационная модель функционирования ОКБ была реализована средствами основной библиотеки среды имитационного моделирования AnyLogic и представлена на рисунке 2.

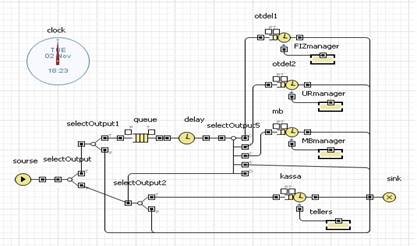
Рисунок 2. Моделирование деятельности Банка

С помощью имитационной модели можно проанализировать и оптимизировать следующие показатели:

-       денежная масса по выданным кредитам и собранным платежам;

-       величина возможной, но не собранной денежной массы в кассе и кредитном отделе от не обслуженных клиентов;

-       максимальная и средняя длина очереди в операционном и кредитном отделе;

-       количество обслуженных и не обслуженных клиентов в операционном и в кредитном отделе;

-       вероятность отказа в обслуживании;

-       коэффициент простоя обслуживаемого канала и объекта;

-       среднее время обслуживания, нахождение и ожидания клиента;

-       «узкие места» работы ОКБ;

-       а также оптимизировать такие параметры как:

-       количество обслуживающих касс, кредитных инспекторов;

-       график работы сотрудников ОКБ.

С использованием построенной модели была проведена серия экспериментов с целью оптимизации структуры операционного отдела ОКБ, и как следствие улучшение финансово-экономических показателей предприятия.

Калибровка модели была выполнена на фактических данных работы отделения № 4201 Банка ОАО «УРАЛСИБ» г. Стерлитамак.

Эксперимент 1. Результаты вычислительного эксперимента по оптимизации количества обслуживающих аппаратов в предположении стационарного входного потока приведены в таблице 2.

Таблица 2.

Исходные данные модели

Вычислительные эксперименты функционирования ОКБ проводились в условиях стационарных и нестационарных входных потоков в предположении работы 2-4 касс. Характеристики входного потока: стационарный; интенсивность потока 0.6; время-720 минут модельного времени. В таблице 3 представим результаты эксперимента 1.

Таблица 3.

Результаты эксперимента 1

Графическая интерпретация результатов эксперимента 1 представлена на рисунках 3-6:

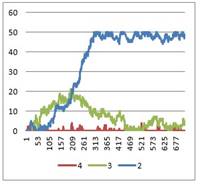
Рисунок 3. Длина очереди в кассе       Рисунок 4. Величина денежной массы

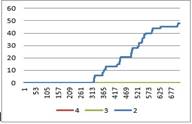
Рисунок 5. Количество клиентов, отказавшихся от обслуживания в кассах

Анализируя графики, величина денежной массы равномерно растет на протяжении всего дня, и на конец работы величина денежной массы равна 765 073 рубля, в случае работы 4 касс; 768 408 рублей, в случае работы 3 касс;682 010рублей, в случае работы 2 касс.

При выборе второго режима работы операционного отдела экономия по выплате зарплаты составляет 15 000 рублей в месяц, или 180 000 рублей в год. При выборе третьего режима работы операционного отдела экономия по выплате зарплаты составляет 30 000 рублей в месяц, или 360 000 рублей в год.

Таким образом, наибольший экономический эффект ­ 360 000 рублей в год составляет при выборе режима работы 3 касс.

На практике, как правило, входной поток клиентов не является стационарным, т.е. его интенсивность меняется в течение дня. Учитывая это, проведем серию вычислительных экспериментов с переменной нагрузкой на обслуживающие каналы. [3]

Эксперимент 2. Оптимизация графика обслуживания клиентов в предположении нестационарного входного потока при работе 3 касс. Результаты эксперимента 2 представлены в таблице 4.

Таблица 4.

Результаты эксперимента 2

Максимальная длина очереди в кассы равна 50 человек или среднем длина очереди в одну кассу не превосходит 15 – 25 человек. Максимальная длина очереди к КИ равна 15 человек.

Графическая интерпретация результатов эксперимента 2 представлена на рисунках 6-9.

Рисунок 6. Величина денежной массы      Рисунок 7. Длина очереди в КИ в кассах

Рисунок 8. Длина очереди в кассы.       Рисунок 9. Величина денежной массы к КИ

В первой и второй ситуациях вероятность отказа по заявке равна нулю. В третьем ситуации 13% заявок остаются не обслуженными. Коэффициент простоя касс в первой ситуации равен 0,069, а значит, 49 минут кассы простаивали. Во второй и третьей ситуации, кассы простаивали около 5 минуты за весь рабочий день. Во всех трех ситуациях, коэффициент загрузки близок к 1, следовательно, работа касс идет непрерывно и равномерно.

Таким образом, для моделирования различных финансовых ситуаций можно применять современные методы и инструменты, снижающие временные и финансовые затраты, одним из которых является метод имитационного моделирования. Имитационная модель дает возможность проверить различные идеи, гипотезы и предположения относительно развития бизнеса, проанализировать последствия их реализации